エクセル関数

・誤差関数

誤差関数は，

\(\Large \displaystyle erf(x) = \frac{2}{\sqrt{\pi}} \int_{0}^x exp \left( - t^2 \right) dt \)

で表すことのできる関数です．

平均０の正規分布の累積分布関数は，

\(\Large \displaystyle \frac{1}{\sqrt{2 \pi \sigma^2}} \int_{- \infty}^x exp \left\{ - \frac{t^2}{2 \sigma^2} \right\} dt \)

なので，誤差関数は，

\(\Large \displaystyle \sigma = \frac{1}{\sqrt{2}} \)，の正規分布（平均０）の2倍，さらに０から，ですね．

\(\Large \displaystyle erf(0) = 0 \)

\(\Large \displaystyle erf(- \infty) = -1 \)

\(\Large \displaystyle erf( \infty) = 1 \)

です．

エクセルでの関数は，

・ERF(x)　：　誤差関数

\(\Large \displaystyle \frac{2}{\sqrt{\pi}} \int_{0}^x exp \left( - t^2 \right) dt \)

と公式通りですが，括弧内のパラメータを二つにすると，

・ERF(a,b)　：　誤差関数（っぽい）

\(\Large \displaystyle \frac{2}{\sqrt{\pi}} \int_{a}^b exp \left( - t^2 \right) dt \)

という計算ができます．これは，

\(\Large \displaystyle = \frac{2}{\sqrt{\pi}} \left[ \int_{a}^0 exp \left( - t^2 \right) dt + \int_{0}^b exp \left( - t^2 \right) dt \right]\)

\(\Large \displaystyle = \frac{2}{\sqrt{\pi}} \left[ - \int_{0}^a exp \left( - t^2 \right) dt + \int_{0}^b exp \left( - t^2 \right) dt \right]\)

\(\Large \displaystyle = erf(b) - erf(a) \)

となります．したがって，

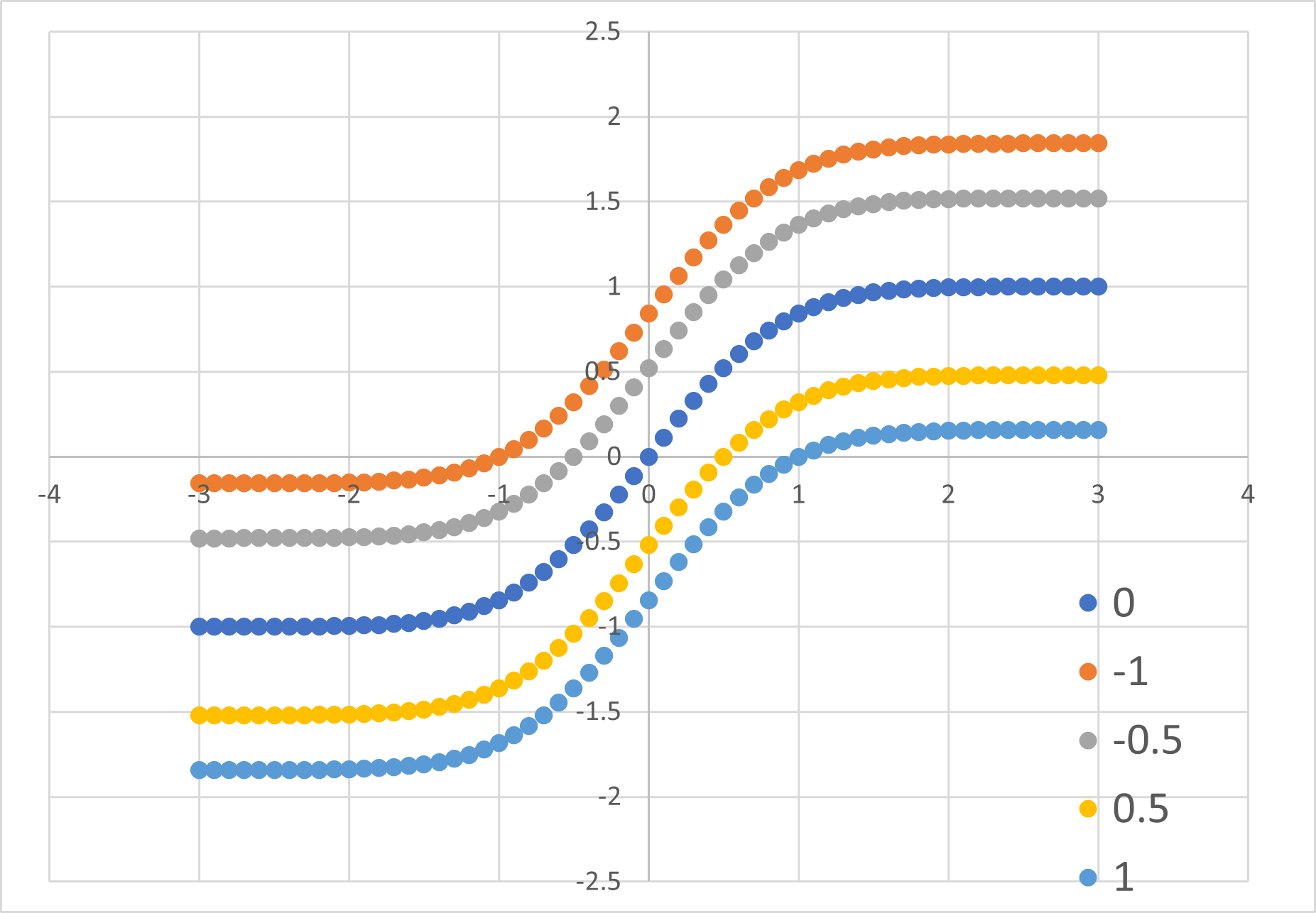
\(\Large \displaystyle erf(a,x) = \frac{2}{\sqrt{\pi}} \int_{a}^x exp \left( - t^2 \right) dt = erf(x) - erf(a) \)

となるので，-erf(a)，だけ下駄をはかせることになります．

・ERF.PRECISE(x)　：　誤差関数

\(\Large \displaystyle \frac{2}{\sqrt{\pi}} \int_{0}^x exp \left( - t^2 \right) dt \)

であり，ERF(x) = ERF.PRECISE(x)，となります．

・ERFC(x)　：　相補誤差関数

\(\Large \displaystyle \frac{2}{\sqrt{\pi}} \int_{x}^{\infty} exp \left( - t^2 \right) dt = 1 - erf(x) \)

・ERFC.PRECISE(x)　：　相補誤差関数

\(\Large \displaystyle \frac{2}{\sqrt{\pi}} \int_{x}^{\infty} exp \left( - t^2 \right) dt = 1 - erf(x) \)

であり，ERFC(x) = ERFC.PRECISE(x)，となります．

なんで結果が同じ関数があるかは不明ですが，たぶん，長期的な関数の統廃合があるのかもしれません．