ドラゴン桜，図形問題-01

ドラゴン桜，もう20年前近くのコミックですが，今見ても面白いですね．

その中で（巻数は忘れちゃいましたが．．）図形問題があり，気になったので解いてみました．

ネットを検索しても関連記事は見つかりませんでした．．．

・問題

問題は，

　円に内接する四角形ABCDで，

\( \Large AB = AD = \sqrt{3}, \ BD = 2 \sqrt{2}, AC = \sqrt{6}, \ cos \angle ABC = \frac{\sqrt{3}}{3} \)

である．このとき，CD = ???

という問題で，教師は，

　図を描いても図が正確でないと線の長さがわからない
　焦らずに丁寧に図を描こう
　見ただけで答えが推測できる
　CDは整数で2よりも明らかに小さいから１だ

と話しています．しかし．．．．

　見ただけでは答えが推測できない．．．．

ので，まずは正確な図を描いてみました．

・作図

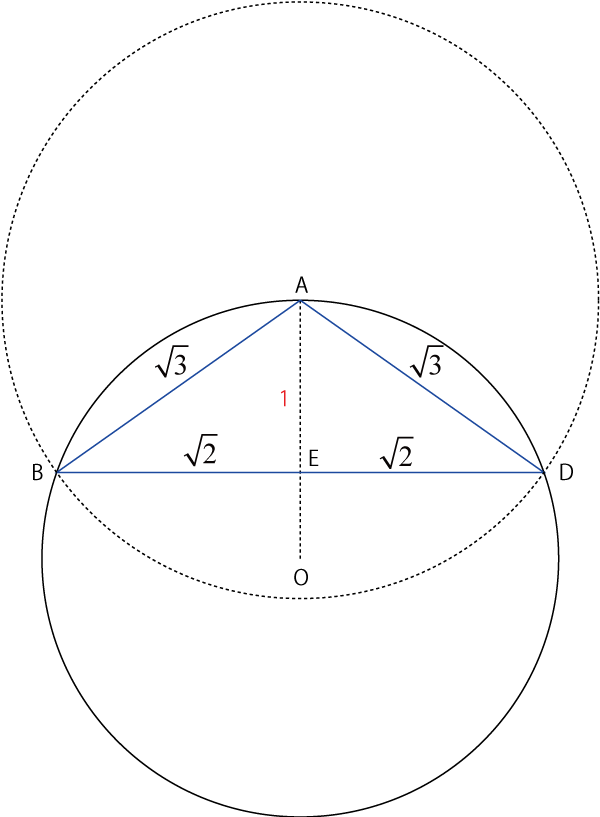
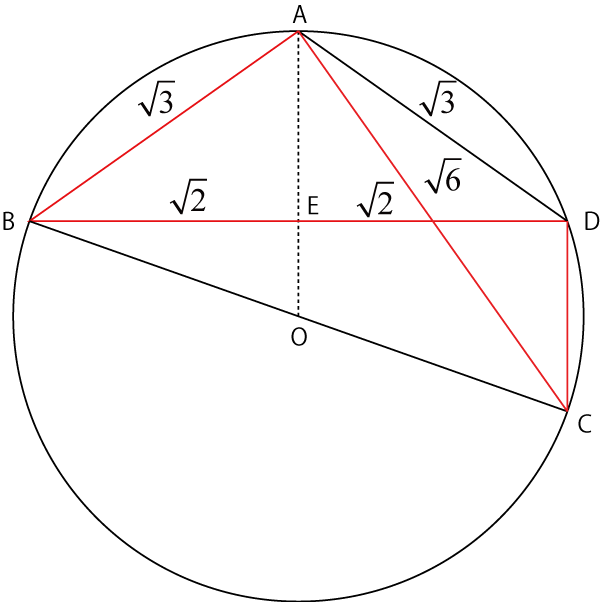
まずはBDの位置を確定します．Aを中心に半径ルート3の円との交点がB，Dとなります．

次に三角形ABDを考えます．これは明らかに二等辺三角形なので，円の中心から伸ばした線による直角三角形の高さAEは，１，となります．

つぎに，三角形BEO，DEO，について考えます．高さは，r－1，なので，

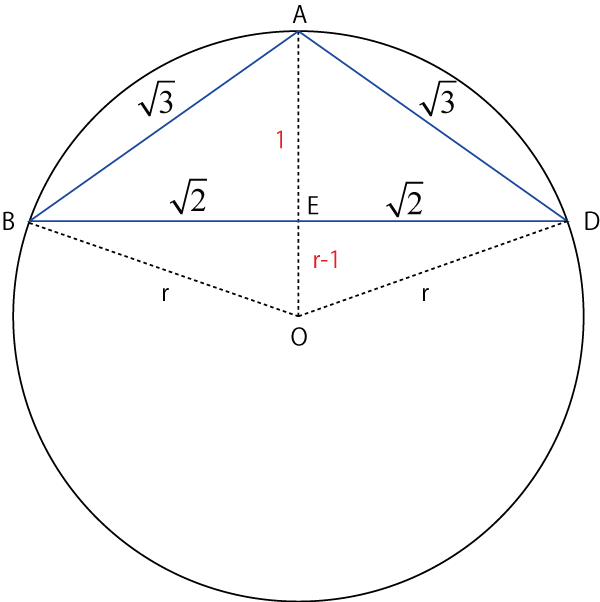
\( \Large r^2 = (r-1)^2+( \sqrt{2})^2 \)

\( \Large r^2 = r^2-2r+1+2 \)

\( \Large 2r = 3 \)

\( \Large r = 1.5 \)

となります．

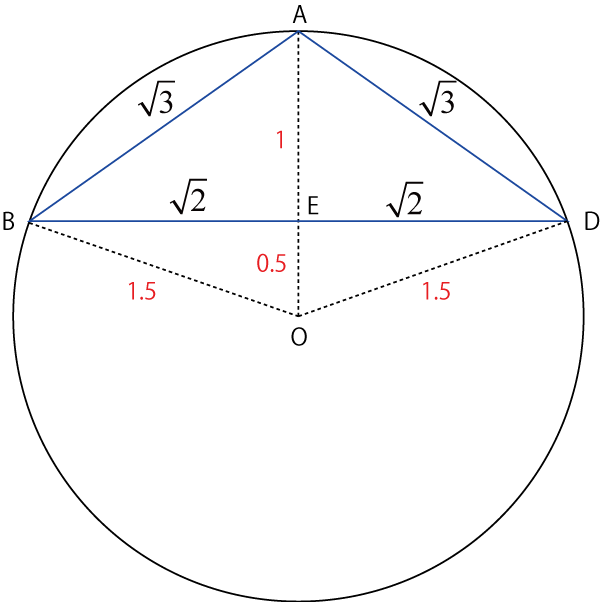
つぎに，Aを中心に半径ルート6の円との交点がCとなります．

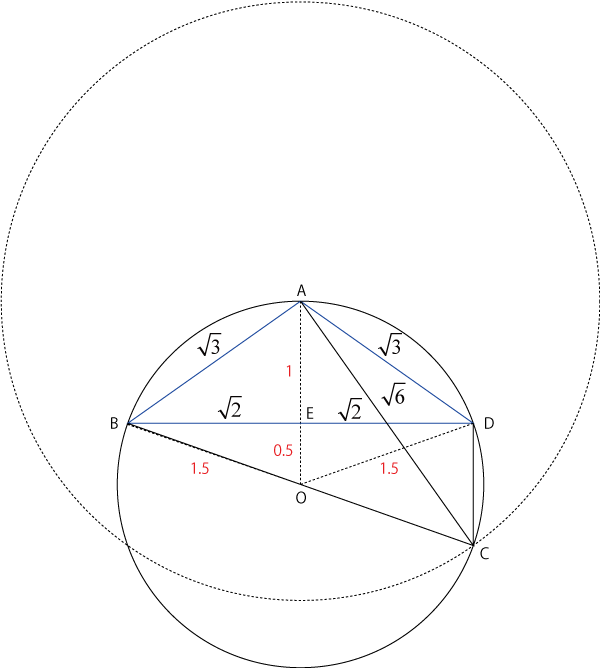
ドラゴン桜の図と比べるとだいぶ異なりますね．．．．図を正確に描く，と言っているのに．．．

四角形ABCDの形が妙にきれいなのが気になりますが．．．

・余弦定理，円周角の定理

余弦定理より，

\( \Large \sqrt{3} = (\sqrt{3})^2 + (2 \sqrt{2})^2 -2 \cdot \sqrt{3} \cdot 2 \sqrt{2} \cdot cos \angle ABD \)

\( \Large \sqrt{3} = (\sqrt{6})^2 + CD^2 -2 \cdot \sqrt{6} \cdot CD \cdot cos \angle ACD \)

したがって，

\( \Large cos \angle ABD = \frac{2}{ \sqrt{6}} \)

\( \Large cos \angle ACD = -\frac{3+CD^2}{ 2 \sqrt{6} CD} \)

円周角の定理より，

\( \Large \angle ABD = \angle ACD \)

したがって，

\( \Large \frac{2}{ \sqrt{6}} = \frac{3+CD^2}{ 2 \sqrt{6} CD} \)

\( \Large CD^2-4 CD+3 = 0 \)

\( \Large (CD-3) (CD-1) = 0 \)

\( \Large CD = 3, 1 \)

となります．

\( \Large cos \angle ABC = \frac{\sqrt{3}}{3} \simeq 0.577 < \frac{ \pi}{4} \)

なので，\( \Large \ \angle ABC \)は，鋭角となります．したがって，AB > CD，となるので，

　CD = 1

という答えとなります．

次ページにいろいろと気になる点を話していきます．