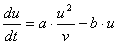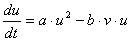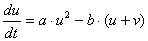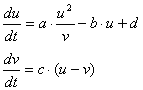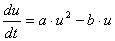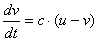|
|
|
双安定系から振動・興奮・空間パターンをつくる
文責:尾崎 淳 |
|
|
最初にアウトラインを示した方が、目的がハッキリして読みやすいと思います。
|
|
右の様に双安定状態を持つ反応系が細胞に入っています。
その細胞が、外部からの操作なしに(この点が大事!)、自律的に安定状態を変えることができるでしょうか?
また多細胞集団になったときに、2つの安定状態が棲み分けて共存(つまり細胞分化)することができるでしょうか?もちろん外部からの操作なしにですよ。
|
|
|

|
|
|
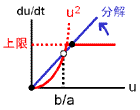
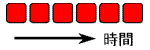
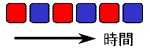
双安定系は2つの安定状態を持ってはいますが、一度どちらかの状態に落ち着くと、それっきりです(右図、左)。
動きがないので“生き生き”としていません。
双安定系にどのような条件を加えたら、“拍動”を始めるでしょうか?(右側)
|
|
|
|
単なる双安定系
|
2状態間を遷移する系
|
|
時間変化
|
 |
 |
|
|

|
|
|
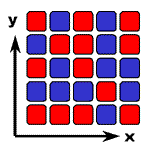
また、2つの安定状態のどちらになるかは初期値に依存するので、初めがランダムならば最終状態もランダムです。
よって双安定系を並べても、互いに相互作用がなければ、最終パターンもランダム・パターンになります(右図、左)。
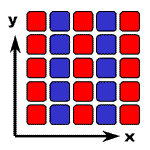
どのような相互作用を加えたら、全体として秩序ある空間パターンを維持できるでしょうか?(右側)
|
|
|
|
ランダム
(相互作用なし)
|
パターン
(相互作用あり)
|
|
空間
パターン
|
 |
 |
|
|

|
|
双安定系を“動かす”
|
次の双安定系を考えます。
aは合成項の係数、bは分解項の係数です。
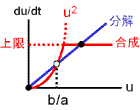
2つの安定状態のうち、値が大きい方をuhigh、小さい方をulowと呼びます(合成-分解のバランス図、黒丸)。
uhigh⇔ulowの間を分ける分岐点はu = b/aです(白丸)。
バランス図とシミュレーション結果を見れば明らかなように、b/aを動かせばuhigh⇔ulowをスイッチングできます。
a≫bならば値はほとんどuhigh、一方a≪bならば値はほとんどulowに行き着きます。
では、どうすれば自律的にスイッチングが起こるでしょうか?
手で動かす、なんてのはダメですよ!
いわゆる“プレ・パターン”っていうのは、外部から操作している訳だから、手で動かしているのと同じです。
生物は外部からの操作なしに、自律的にニョキニョキ・ドクドクし始めるんです。
“プレ・パターン”なるものは、何の説明にもなっていません!
|
|
|
|

|
|
調節因子のとるべき条件
|
スイッチングを起こす調節因子vを導入します(右図)。
vの合成は、uが促進するものとします。
|
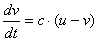 |
(*) |
調節因子はuhigh⇔ulow間を遷移させなければなりません。つまり、
|
uhighのとき → 合成を弱める、もしくは分解を強める |
|
かつ |
|
ulowのとき → 合成を強める、もしくは分解を弱める |
を同時に満たさなければいけません。これも負のフィードバックの一種ですよね。
|
|
この条件を満たす最もシンプルな形として、合成項に a∝1/v で作用する
|
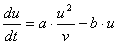 |
(1) |
もしくは分解項に b∝v で作用する
|
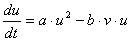 |
(2) または |
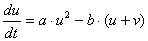 |
(3) |
が考えられます。
反応拡散系をまじめに勉強した経験のある人は気付いたと思います。(1)式はGierer-Meinhardtの式と言われているものです。
|
双安定系+調節因子⇒ダイナミズム
いよいよニョキニョキ・ドクドクが生まれます。
どの式を使っても結果は同じですが、ここでは(1)と(*)式を使います。
ここで、濃度に依存しない合成項dを加えました。
これは、反応速度が濃度のみに依存する形にすると、ulow=0になったときに、系がそれ以上変化しなくなってしまうからです。
|
|
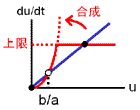
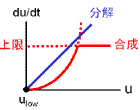
また、ここでは調節因子vの効果を調べたいので、双安定系のパラメータは固定します(a=8, b=10, 合成速度の上限=10)。
このときの双安定系の合成-分解のバランスは右図のようになっています。
つまり、調節因子なしの現時点では、ulow=0のみの単安定状態になっています。
|
|
|

|
|
|
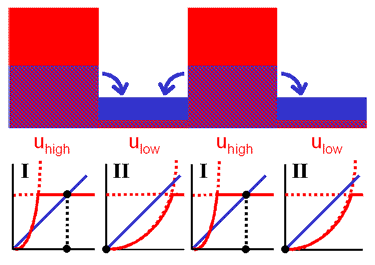
この状態にvの効果を加えると双安定状態が復活します。
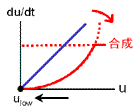
uの値が大きいとき、vも大きくなるので合成項が弱まります(右図、状態 Ι)。
結果、ulowに向かって減少していきます。
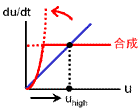
逆に、uの値が小さいとき、vも小さくなるので合成項が強まります(右図、状態 ΙΙ)。
このときは、uhighに向かって増大していきます。
|
|
状態 Ι
uが大きいとき
|
 |
|
状態 ΙΙ
uが小さいとき
|
 |
|
|

|
|
(1) 振動・興奮
この様に場合ごとに分けて考えると、もうそれだけで振動が起こることは明らかだと思います。しかし、必ずしも事はそう簡単にはいかないことも示します。
|
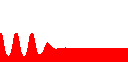
まず基礎合成がない場合(d=0)を見ます。
このときはulow=0で合成項が0になってしまうので、それ以上何も起こりません(右図:u, v以下同じ)。
調節因子の反応速度が遅いとき(c=1)は、想像通り、uhigh(=1)を通ってulowまでデジタルに1回“振動”しています。
ところがc=10のときはどうでしょう?
一瞬ピョコっと上がるだけで、すぐにulowに収束してしまいました。
|
|
|
d=0
|
横軸:時間 |
|
c=1
|
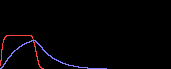 |
|
c=10
|
 |
|
|

|
|
|
これが(以前言った)「あぁなって、こうなって」法の限界なのです。
c=1のときは、vの“タイムラグ”の効果で振動性が生まれています(これも以前に説明しましたね)。
vの反応が遅いので、まず完全にuがuhighに行き着いてから(状態 Ι)、ついで状態 ΙΙが進行しています。
個々のできごとを分離できるので、頭で考えても想像しやすいのです。
しかしc=10の場合、vの反応が早いので、状態 Ιと状態 ΙΙのできごとがほぼ同時に進行してしまっています。
2つのイベントが同時進行するような反応は、人間の頭ではなかなか想像するのは難しいのです(シミュレーションの出番)。
|
|
上の様な1回きりの“振動”のことを興奮現象といいます。
神経パルスなどが、これにあたります。
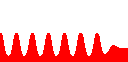
次に基礎合成を加えます(d≠0)。
すると持続的な振動(リミット・サイクル)が生まれます。
つまり振動とは、基礎合成のお陰で、連続的に“興奮”していることなのです。
ところがc=10では、uhighでもulowでもない第3の状態に収束してしまいました。
こんなことはシミュレーションしてみないと分からない結果ですよね?
|
|
|
d=1
|
横軸:時間 |
|
c=1
|
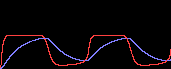 |
|
c=10
|
 |
|
|

|
|
(2) 空間パターン
振動の項で、(d=1, c=10)のとき、uは双安定系らしからぬ第3の値に収束してしまいました。
実は、この第3の状態は多細胞系に移すと、さらに生物学的に魅力ある状態を生みます。
パターン形成です。
|
|
右図のような状況を設定します。
いままでは単細胞での時間変化を見てきましたが、この節では、それらの細胞を1次元上に並べて、分子(u, v)が互いに行き来できるようにします。
分子の動きやすさは拡散速度(Du, Dv)で表します。
|
|
|

|
|
|
以下の1次元シミュレーションでは100個の細胞が並べてあります。
再び基礎合成がない場合(d=0)から話を始めます。以下では(c=10, Du=1)に固定します。
さらにここでは次のような摂動を加えてみます。
系が安定状態(ulow=0)に至った時点で、左端の細胞に少しだけuを足します(極微量)。
多細胞系では、どのようなダイナミクスが生まれるでしょうか?
u, vの拡散速度に差がない場合(Dv=1)、(おそらく、ほとんどの人の常識どおり)すぐにulow=0に落ち着きます。
ところがDv=10にすると1本だけピークが立ち上がりました。
なんでしょうね、これは?
|
|
|
d=0
|
横軸:座標 |
|
Dv=1
|
 |
|
Dv=10
|
 |
|
|

|
|
|
答えは後回しにして、
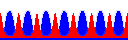
次にパラメータ(c=10, Du=1, Dv=10)に基礎合成を加えます(d=1)。
つまり、振動の項で“第3の安定状態”をとったときのパラメータです。
こんどは、ピークは1本だけではなく、次々と周期パターンを作ってしまいました(右図、上から下へ時間経過)。
これがいわゆる“チューリング・パターン”や“反応拡散波”と呼ばれるものです。
どうしてこんなことが起こるのでしょうね?
|
|
|
|

|
|
振動と周期パターンは“同じ”原理で生まれる
実は振動も周期パターンも同じ「双安定状態間の遷移」が生み出したものなのです。
|
|
まとめると右図のようになります。
横軸は、振動では時間、周期パターンでは座標です。
復習すると・・
2つの安定状態(uhigh, ulow)は2タイプの合成-分解バランス(状態 Ι, 状態 ΙΙ)によって、それぞれ生まれます。
調節因子vが、この2つの状態間を遷移させます。
振動では、調節因子の遅い反応性によって“少し後”を逆の状態に誘導します(振動の項、参照: uhigh→ulow→uhigh→ulow)。
時間の流れは一方向だから、振動の場合は左から右への矢印のみ。
|
|
|

|
|
|
一方、周期パターンでは、調節因子の速い拡散が“少し隣”を逆の状態に誘導しているのです。
ついでにu, vの拡散速度が同じ場合も併せて考えてみてください。双安定状態に分離できないことが分かると思います。
これは振動の場合と同じです。
振動では、調節因子の反応速度が速いときは、uとvの反応がほぼ同時進行するので2状態が(時間的に)分離しなかったですよね(第3の状態)。
空間パターンの場合では、uとvの拡散がほぼ同じだと2状態が(空間的に)分離しないのです。
つまり、まとめると「反応速度や拡散速度が極端に違うフィードバックがからむと、振動やパターンなどの複雑な現象が生まれる」ということです。現実の生体反応を考えれば、そんなことよくあることでしょ。
おそらく、振動のメカニズムは容易に理解できるが空間パターンになると「?」と考えてしまう人が多いことでしょう。
理解に詰まるところは人それぞれなので理解のツボを強要はできませんが、私の場合は最初、ulowの周りになぜuhighが誘導されるのかが理解できませんでした。
一方、uhighの周りにulowが誘導されるのは、生物学ですでに知られている“Lateral Inhibition”のことなので、何となく解かるでしょう。
解からなかった原因は “uhigh=パターンがあるところ、ulow=パターンがないところ” だとイメージしていたからです。
突破口は、(uhigh, ulow)は互いに双安定系を構成する相補的な関係であり、どちらが“上”だなんてことはない、ということに気付いたことです。
人はついつい勝手に“地”と“柄”をつくって対象を見てしまいます。
あなたが注目しているin situパターン、それは“地”ですか“柄”ですか?・・そんなもの無いのかもよ。
とにかく大事なイメージは 振動&パターンは、自律的に分離する双安定状態だ ということです(下記、「周期性のないパターン」の項、参照)。
この図では分かりやすくするためにuの拡散を0にしています。
だからパターンは完全にデジタルです。
uも拡散できるようにするとパターンは滑らかになります(上のシミュレーション)。
また、拡散速度が周期性(ピークとピークの間隔)を決めていることも分かると思います(逆状態への誘導が及ぶ範囲が周期を決める)。
状態遷移を循環させる(周期性を持たせる)ためには、基礎合成が必要です(d≠0)。
基礎合成がないと、興奮現象や1本のみのピークが生まれます。
ちなみに、1本ピークって、要は“モルフォゲン勾配”ってことですよね(→総説(PDF, 1.5M))。
|
|
これまでに挙げた例は、わかりやすく見せるために、典型的なダイナミクスを生むパラメータを使っています。
それらを組み合わせれば、より複雑なパターンを生むことができます。
有名な例は“移動波”です(神経パルスは、これ)。
移動波では、時間・空間ともに“近傍を逆状態に誘導”することにより生まれます。
ともに・・と言うか、もはや分けることに意味はないな。横軸を時間軸と見るか座標軸と見るかの違いだけだから。大事なのは“遷移する双安定系”、ただそれだけです。
|
|
|

|
横軸:座標 |
|
d=0
c=5
Dv=1
|
 |
|
|

|
|
空間パターンのバリエーション
(1) 3変数系
|
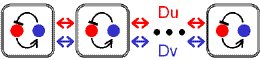
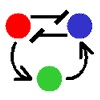
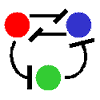
フィードバック&双安定系のページでも言ったように、互いに抑制しあう2変数系でも双安定系は作られる(右図、赤-青)。
これに調節因子(緑)を加えた3変数系でも、もちろん振動および空間パターンは作られる。
この場合、2変数系でのuhigh, ulowに相当する状態は(赤high, 青low)と(赤low, 青high)の2状態になる。
調節因子による“逆状態への遷移”方法には2通りある。“「相手を誘導する」のを「誘導する」”か“「相手を抑制する」のを「抑制する」”かである。
後者の場合ならば、ネットワークは全て負のフィードバックから成り立っている。
このように組んで行けば、バリエーションはいくらでもあることが分かるだろう。
|
誘導の誘導 |
抑制の抑制 |
 |
 |
|
|

|
|
|
相互抑制系の場合、uとvはキレイに相補的に分布する(右図)。
ショウジョウバエの分節境界では、このメカニズムが働いていると考えられている(Meinhardt)。
|
|
|

|
|
(2) 周期性のないパターン(ウシ柄)
多くの反応拡散系の解説本では、チューリング・パターンのでき方は、
「均一な状態」+「大きい拡散速度の比」⇒「周期パターン」
という書き方なので、反応拡散パターンは周期パターンのみしか作れないと思っている人もいるのではないだろうか?
その様な印象を与える大きな原因は、最終的にできるパターンは双安定系である、ということを明快に記述していないからである。
チューリング・パターンができる瞬間に何が起こっているのか?を端的に言うならば、
「双安定状態にない“双安定系”」+「大きい拡散速度の比」⇒「双安定状態の復活」
と言うべきである。
「パターン」と「周期パターン」とは別物です。
広義の反応拡散パターンとは周期パターンのみを意味するわけではありません。
そのことは、双安定系を前面に押し出して見れば分かります。
下図は、すでに双安定状態にある系に拡散の効果のみを変化させた場合の2次元パターンです。
拡散なし(細胞同士の相互作用なし)のときは、2状態どちらかをとるランダム・パターンになります(左端)。
Dv/Du=1で拡散を加えると、ややuhighが多いところは周りの細胞もuhighに、ややulowが多いところでは周りの細胞をulowに誘導し、結果、“まだら模様”・“ブチ柄”になります(左から2つ目)。
これが、双安定系がつくるパターンの基本です。
遺伝子スイッチ(双安定系)を空間的に広げるだけで、とりあえずパターンは出来るんですよ。でも、こんな大事(かつ当たり前)なことをちゃんと書いてある教科書ってないですよねぇ。
“細胞分化”(=双安定系)とか“パターン形成”(=双安定系を空間的に広げたもの)とかいう概念をバラバラに述べるのではなく、このように体系的に書けないものですかね?
次に徐々に拡散速度の比を大きくしていきます。
段々と周期性(等間隔性)が現れるのが分かると思います。
なぜ周期性が生まれるのかは、すでに説明しました(調節因子が近傍を逆状態に誘導する)。
狭義のチューリング・パターンとは、この周期パターンのことを言っています。
|
Du = 0 |
Dv/Du = 1 |
Dv/Du = 2 |
Dv/Du = 5 |
Dv/Du = 10 |
 |
 |
 |
 |
 |
|
以上で終わりです。フィードバックを出発点に、何の無理な仮定も加えずに、ここまで表現できるのです。
|
“Under these circumstances, one would be surprised if Nature had made no use of this possibility” (Dirac, P.A.M.)
|