慣性モーメント

平行軸の定理の検証

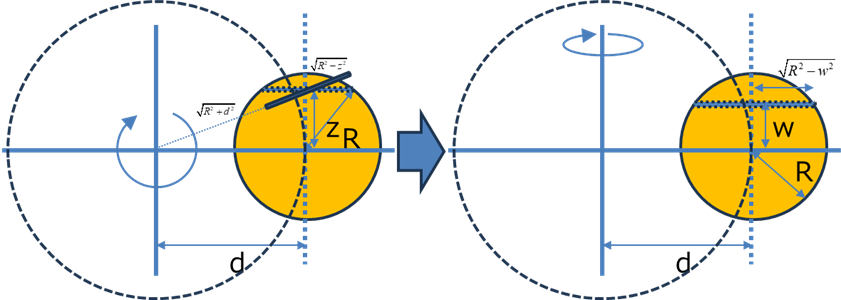
・球の場合

球の場合，棒の慣性モーメントの求め方が基本となりますが，前ページの円板（水平）を元に計算していきます．

密度を導入する前の円板（水平）の慣性モーメントは，上左図のように，

\( \Large \displaystyle J_{disk} = \rho \left[ \pi d^2 R^2 + \frac{ \pi}{2} R^4 \right] \)

となりますが，90度回転させて，回転軸を横から見ると，このRがｗによって変わるので，

\( \Large \displaystyle \sqrt{ R^2 - w^2} \)，としてーRからRまで積分することになります．

\( \Large \displaystyle J_{sphere} = \rho \int_{-R}^R \left[ \pi ( \sqrt{ R^2 - w^2})^2d^2 + \frac{ \pi}{2} ( \sqrt{ R^2 - w^2})^4 \right] \ dw\)

を計算すればいいことになります．第一項と第二項に分けて考えます．

・第一項

\( \Large \displaystyle J_{1} = \pi d^2 \int_{-R}^R ( R^2 - w^2) \ dw\)

\( \Large \displaystyle J_{1} = 2 \pi d^2 \int_{0}^R ( R^2 - w^2) \ dw\)

\( \Large \displaystyle J_{1} = 2 \pi d^2 \left[ R^2 w - \frac{1}{3} w^3 \right]_0^R \)

\( \Large \displaystyle J_{1} = 2 \pi d^2 \left[ R^3 - \frac{1}{3} R^3 \right] \)

\( \Large \displaystyle J_{1} = 2 \pi d^2 \frac{2}{3} R^3 = \frac{4}{3} \pi d^2 R^3\)

・第二項

\( \Large \displaystyle J_{2} = \frac{ \pi}{2}\int_{-R}^R ( R^2 - w^2 )^2 \ dw\)

\( \Large \displaystyle = 2 \ \frac{ \pi}{2}\int_{0}^R ( R^4 - 2 R w^2 + w^4) \ dw\)

\( \Large \displaystyle = \pi \left[ R^4w - 2 R \frac{1}{3} w^3 + \frac{1}{5} w^5 \right]_0^R\)

\( \Large \displaystyle = \pi \left[ R^5 - \frac{2}{3} R^5 + \frac{1}{5} R^5 \right] \)

\( \Large \displaystyle = \pi \left[ \frac{15}{15} R^5 - \frac{10}{15} R^5 + \frac{3}{15} R^5 \right] \)

\( \Large \displaystyle = \frac{8}{15} \pi R^5 \)

まとめると，

\( \Large \displaystyle J_{sphere} = \rho \left[ \frac{4}{3} \pi d^2 R^3 + \frac{8}{15} \pi R^5 \right] \)

球の質量は体積密度ρを使って，

\( \Large \displaystyle M = \frac{4}{3} \pi \rho R^3 \)

となるので，

\( \Large \displaystyle J_{sphere} = \frac{3}{4} \frac{M}{ \pi R^3} \left[ \frac{4}{3} \pi d^2 R^3 + \frac{8}{15} \pi R^5 \right] = \boldsymbol{Md^2 + \frac{2}{5} MR^2}\)

となり，第一項が平行軸の定理，第二項が球の慣性モーメントとなり，平行軸の定理と一致します．