慣性モーメント

平行軸の定理の検証

棒の場合

・棒の場合-斜め_02

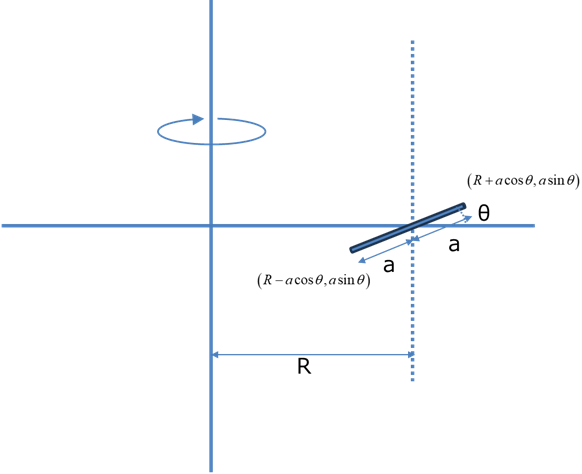
斜めの棒の場合を考えます．回転軸に対して角度θで斜めとなる場合です．

上の図は回転軸上から見た図となります

長さ2aの棒の両端の座標は，回転中心を原点とすると，

\( \Large \displaystyle ( R + a \ cos \theta, a \ sin \theta )\)

\( \Large \displaystyle ( R - a \ cos \theta, -a \ sin \theta)\)

ので，回転軸からの棒の各位置の座標は，ｘ座標だけを考えればいいので，

\( \Large \displaystyle x = R + s \ cos \theta \)

\( \Large \displaystyle ( -a \leq s \leq a )\)

線の場合の密度の定義は，線密度として，長さ２aの場合，

\( \Large \displaystyle M= 2a \rho \)

ですので，慣性モーメントは，

\( \Large \displaystyle J = \int_{-a}^a \left( R + s \ cos \theta \right)^2 \rho \ ds \)

\( \Large \displaystyle J = \int_{-a}^a \left( R^2 + 2 R \ s \ cos \theta + s^2 \right) \rho \ ds \)

\( \Large \displaystyle J = \rho \ \left[ R^2s + Rs^2 \ cos \theta + \frac{s^3}{3} \ cos^2 \theta \right]_{-a}^a \)

第二項は０となるので，

\( \Large \displaystyle J = \rho \ \left[ R^2s + \frac{s^3}{3} \ cos^2 \theta \right]_{-a}^a \)

\( \Large \displaystyle J = \rho \ \left[ 2R^2a + \frac{2 a^3}{3} \ cos^2 \theta \right] \)

\( \Large \displaystyle J =\frac{M}{2a} \ \left[ 2R^2a + \frac{2 a^3}{3} \ cos^2 \theta \right] \)

\( \Large \displaystyle J =MR^2 + \frac{1}{3} Ma^2 \ cos^2 \theta \)

となり，第一項が平行軸の定理，第二項が重心を中心に回転する斜めの棒の慣性モーメントとなり，平行軸の定理と一致します．

次ページは，円板（団扇）の平行軸の定理の検証，を検討していきます．