慣性モーメント

棒

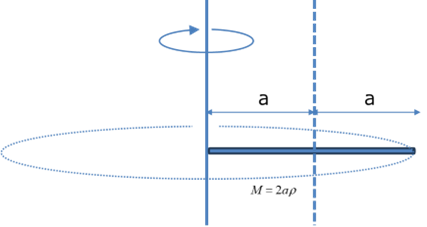
・棒の中心が回転軸の場合

長さ，2a，で重心位置を中心に回転する場合の慣性モーメントを求めていきます

ここでは，断面，太さを考えませんので，質量M，の場合，線密度ρとの関係は，

\( \Large \displaystyle M = 2a \ \rho \)

となります．

回転中心を線の重心，ｘ座標でいうと０，とすると，慣性モーメントは，

\( \Large \displaystyle J = \int_{-a}^a x^2 \rho \ dx = \rho \left[ \frac{x^3}{3} \right]_{-a}^a = \rho \frac{2}{3} a^3 \)

線密度と質量との関係を導入すると，

\( \Large \displaystyle J = \frac{M}{2a} \frac{2}{3} a^3 = \boldsymbol{\frac{1}{3} Ma^2} \)

となります．

・棒の端が回転軸の場合

上と同じ条件，長さ，2a，ですが，棒の端が回転軸の場合を考えていきます．積分範囲が異なり，

\( \Large \displaystyle J = \int_{0}^{2a} x^2 \rho \ dx = \rho \left[ \frac{x^3}{3} \right]_{0}^{2a} = \rho \frac{8}{3} a^3 = \frac{M}{2a} \frac{8}{3} a^3 = \boldsymbol{\frac{4}{3} Ma^2}\)

と重心が回転軸の場合に比べて，4倍，慣性モーメントが大きくなります，すなわち回しにくくなっていることになります．

後に述べる，平行軸の定理，を使えば，回転軸と重心との距離は，a，となりますので，

\( \Large \displaystyle J = \frac{1}{3} Ma^2 + Ma^2 = \boldsymbol{\frac{4}{3} Ma^2}\)

と一致します．

次ページは，斜めの棒の慣性モーメント，を検討していきます．