球体の発熱による温度分布-熱伝導率が異なる細胞膜が存在する場合-21

細胞には細胞膜が存在します．

基本的には，脂質ですので，そう変わった物質ではないですが，細胞膜の熱伝導率を考慮に入れたらどうなるでしょう？

基本的には，同じです．

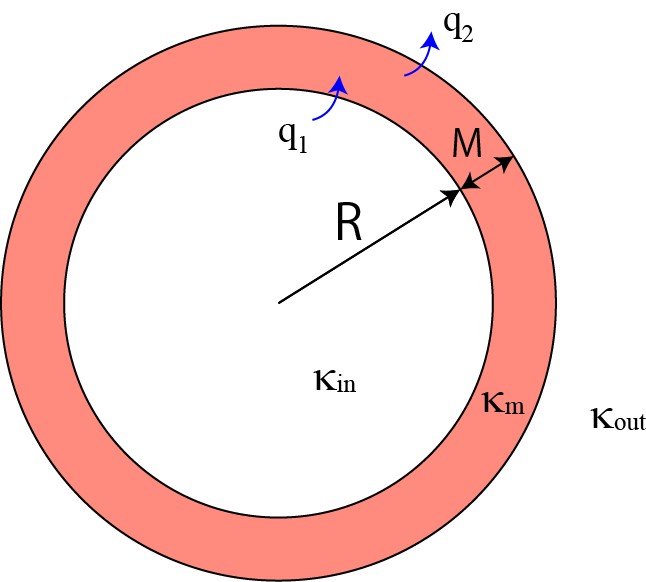
上記のようなモデルを考えてみます．
　厚みMの細胞膜（熱伝導率はκ_m）
が存在し，
　半径Rの細胞と細胞膜との界面で熱q₁
　半径R+Mの細胞+細胞膜と外界との界面で熱q₂
が流れるとします．

各境界の熱の流出量

細胞と膜との間は，

\(\Large q_1 = \frac{pV}{S} = p \frac{\frac{4}{3} \pi R^3}{4 \pi R^2} = \frac{pR}{3} \)

膜と外界との間は，

\(\Large q_2 = \frac{pV}{S} = p \frac{\frac{4}{3} \pi R^3}{4 \pi (R+M)^2} = \frac{pR^3}{3 (R+M)^2} \)

となります．

まずは，簡単な方から．

球の外側の熱拡散方程式

\(\Large - \kappa_{out} \frac{1}{r^2} \frac{d}{dr} (r^2 \cdot \frac{dT_{out}}{dr}) = 0 \)

\(\Large \frac{d}{dr} (r^2 \cdot \frac{dT_{out}}{dr}) = 0 \)

\(\Large r^2 \cdot \frac{dT_{out}}{dr} = C_5 \)

\(\Large \frac{dT_{out}}{dr} = \frac{C_5}{r^2} \)

\(\Large T_{out} = -\frac{C_5}{r} + C_6\)

となります．

r→∞の条件においては，球からの熱の影響を受けず室温（R.T.）となるとすると，

\(\Large T_{out} = -\frac{C_5}{r} + R.T.\)

となります．

ここでも，R+Mでの熱流量から，

\(\Large \frac{dT_{out}}{dr} \vert_{r=R+M} = \frac{C_5}{(R+M)^2} = -\frac{q_2}{\kappa_{out}} = - \frac{p \ R^3}{3 \kappa_{out} (R+M)^2} \)

\(\Large C_5 = - \frac{p \ R^3}{3 \kappa_{out}} \)

となるので，

\(\Large T_{out} = \frac{p \ R^3}{3 \kappa_{out}} \frac{1}{r} + R.T.\)

と記述できます．

つまり，
　熱源である球の外の温度変化は，距離rに反比例して減少する
ことになります．

細胞膜の熱拡散方程式

細胞膜も熱源ではないので，上記の球の外側と同様の計算ができます．
ただ，異なるのが，境界条件が異なり，
　細胞膜外側で細胞外部の温度と等しくなる
という点です．

\(\Large - \kappa_{m} \frac{1}{r^2} \frac{d}{dr} (r^2 \cdot \frac{dT_{m}}{dr}) = 0 \)

\(\Large \frac{d}{dr} (r^2 \cdot \frac{dT_{m}}{dr}) = 0 \)

\(\Large r^2 \cdot \frac{dT_{m}}{dr} = C_3 \)

\(\Large \frac{dT_{m}}{dr} = \frac{C_3}{r^2} \)

\(\Large T_{m} = -\frac{C_3}{r} + C_4\)

となります．

ここでも，r=R+Mでの熱流量から，

\(\Large \frac{dT_{m}}{dr} \vert_{r=R+M} = \frac{C_3}{(R+M)^2} = -\frac{q_2}{\kappa_{m}} = - \frac{p \ R^3}{3 \kappa_{m} (R+M)^2} \)

\(\Large C_3 = - \frac{p \ R^3}{3 \kappa_{m}} \)

となるので，

\(\Large T_{m} = \frac{p \ R^3}{3 \kappa_{out}} \frac{1}{r} + C_4 \)

と記述できます．r=R+Mにおいて温度が一致するので，

\(\Large T_{m} \vert_{r=R+M} = T_{out} \vert_{r=R+M} \)

\(\Large \frac{p \ R^3}{3 \kappa_{m}} \frac{1}{R+M} + C_4 = \frac{p \ R^3}{3 \kappa_{out}} \frac{1}{R+M} + R.T.\)

\(\Large C_4 = \frac{p \ R^3}{3 (R+M)} \left[ \frac{1}{\kappa_{out}} - \frac{1}{\kappa_m} \right] + R.T. \)

従って，

\(\Large T_{m} = \frac{p R^3}{3 \kappa_{m}} \frac{1}{r} + \frac{p \ R^3}{3 )R+M)} \left[ \frac{1}{ \kappa_{out}} -\frac{1}{\kappa_{m}} \right]+ R.T. \)

となります．

球の内側の熱拡散方程式

\(\Large - \kappa_{in} \frac{1}{r^2} \frac{d}{dr} (r^2 \cdot \frac{dT_{in}}{dr}) = p \)

\(\Large \frac{d}{dr} (r^2 \cdot \frac{dT_{in}}{dr}) = - \frac{p \ r^2}{\kappa_{in}} \)

\(\Large r^2 \cdot \frac{dT_{in}}{dr} = - \frac{1}{3} \frac{p \ r^3}{\kappa_{in}}+C_1 \)

\(\Large \frac{dT_{in}}{dr} = - \frac{1}{3} \frac{p \ r}{\kappa_{in}}+ \frac{C_1}{r^2} \)

ここで，前出のr=Rの場合の熱流量と組み合わせると，

\(\Large \frac{dT_{in}}{dr} \vert_{r=R} = - \frac{1}{3} \frac{p \ R}{\kappa_{in}}+ \frac{C_1}{R^2} = - \frac{p \ R}{3 \kappa_{in}}\)

\(\Large \frac{C_1}{R^2} = - \frac{p \ R}{3 \kappa_{in}} + \frac{p \ R}{3 \kappa_{in}} =0 \)

となり，C₁=0，となります．従って，

\(\Large \frac{dT_{in}}{dr} = - \frac{1}{3} \frac{p \ r}{\kappa_{in}} \)

\(\Large T_{in} = - \frac{1}{6} \frac{p \ r^2}{\kappa_{in}} +C_2\)

となります．

r=Rにおいて細胞膜の温度が一致するので，

\(\Large T_{in} \vert_{r=R} = T_{m} \vert_{r=R} \)

\(\Large - \frac{1}{6} \frac{p \ R^2}{\kappa_{in}} +C_2 = \frac{p R^3}{3 \kappa_{m}} \frac{1}{R} + \frac{p \ R^3}{3 (R+M)} \left[ \frac{1}{ \kappa_{out}} -\frac{1}{\kappa_{m}} \right]+ R.T. \)

\(\Large \begin{align*} C_2 &= \frac{1}{6} \frac{p R^2}{\kappa_{in}} + \frac{p R^2}{3 \kappa_m} + \frac{p R^3}{3 (R+M)} \left[ \frac{1}{ \kappa_{out}} - \frac{1}{\kappa_m} \right] + R.T. \\
&= \frac{p R^2}{6} \frac{2}{ \kappa_{in}} + \frac{p R^2}{3 \kappa_m} + \frac{p R^3}{3 (R+M)} \left[ \frac{1}{ \kappa_{out}} -\frac{1}{\kappa_m} \right] + R.T. \end{align*} \)

となるので，

\(\Large T_{in} = - \frac{1}{6} \frac{p r^2}{\kappa_{in}}
+ \frac{p R^2}{6} \left[ \frac{1}{ \kappa_{in}} + \frac{2}{\kappa_m} \right]
+ \frac{p R^3}{3 (R+M)} \left[ \frac{1}{ \kappa_{out}} - \frac{1}{\kappa_m} \right] + R.T. \)

となります．

まとめ

\(\Large T_{out} = \frac{p \ R^3}{3 \kappa_{out}} \frac{1}{r} + R.T.\)

\(\Large T_{m} = \frac{p R^3}{3 \kappa_{m}} \frac{1}{r} + \frac{p \ R^3}{3 )R+M)} \left[ \frac{1}{ \kappa_{out}} -\frac{1}{\kappa_{m}} \right]+ R.T. \)

\(\Large T_{in} = - \frac{1}{6} \frac{p r^2}{\kappa_{in}}
+ \frac{p R^2}{6} \left[ \frac{1}{ \kappa_{in}} + \frac{2}{\kappa_m} \right]
+ \frac{p R^3}{3 (R+M)} \left[ \frac{1}{ \kappa_{out}} - \frac{1}{\kappa_m} \right] + R.T. \)

次に，具体的な値を入れてみましょう．