化学平衡論

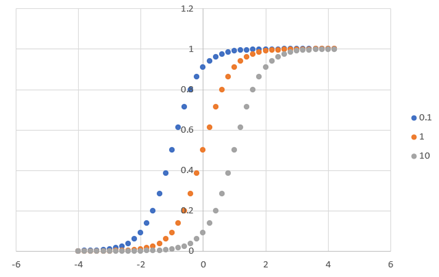
基質の結合曲線，リニア vs. 対数表示

[L]=Kの時の傾きは，

リニア表示の場合，

\( \Large \displaystyle \left. \frac{d \ P_B}{dL} \right|_{[L]=K} = \frac{K}{(K +K)^2 } = \frac{1}{4K}\)

とKに依存します．

対数表示の場合は，

\( \Large \displaystyle \left. \frac{d \ P_B}{dL} \right|_{[L]= K} = \frac{2.3}{4} = \frac{1}{ 4 \ log (e)} = 0.575 \)

とKに依存しないことがわかります．

これら両者の関係は，

\( \Large \displaystyle \left. \frac{d \ P_B}{dL} \right|_{[L]=K} = \left. \frac{d \ P_B}{d \ log \ L} \frac{d \ log \ L} {L} \right|_{[L]=K}
= \left. \frac{d \ P_B}{d \ log \ L} \right|_{[L]=K} \left. \frac{d \ log \ L} {L} \right|_{[L]=K}\)

となります．

\( \Large \displaystyle \left. \frac{d \ log \ L} {L} \right|_{[L]=K}\)

ですが，

\( \Large \displaystyle log \ L = y \rightarrow L = 10^y \rightarrow ln \ L =ln \ 10^y = y \cdot ln 10 = \frac{ln L}{2.3} \)

なので，

\( \Large \displaystyle \left. \frac{d \ log \ L} {L} \right|_{[L]=K} =\frac{1}{2.3} \left. \frac{d \ ln \ L} {L} \right|_{[L]=K} = \frac{1}{2.3 K} \)

となるので，

\( \Large \displaystyle \left. \frac{d \ P_B}{dL} \right|_{[L]=K} = \left. \frac{d \ P_B}{d \ log \ L} \right|_{[L]=K} \frac{1}{2.3 K} \)

となり，それぞれ，

\( \Large \displaystyle \frac{1}{4K} = \frac{2.3}{4} \frac{1}{2.3 K} \)

となり，一致することがわかります．

対数表示にすると，

環境が変化すると，解離定数Kが変わったときに，カーブがシフトすることからわかりやすくなりますね．

しかし，横軸の基質濃度が対数なので，
　幅広い濃度域での実験
が必要となり，さらに，
　変曲点での濃度域での実験
が必要となります．

ちなみに，1～10の濃度範囲（ｍMでもμMでもなんでも）では，

と１～4の範囲を重点的に実験することが必要となります．