化学平衡論

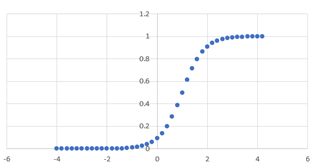
基質の結合曲線，対数表示

\( \Large \displaystyle P_B = \frac{[L]}{K + [L] } \)

を並べ替えて，

\( \Large \displaystyle [L] = P_B \cdot K + P_B \cdot [L] \)

\( \Large \displaystyle [L] = \frac{P_B \cdot K}{1 - P_B } \)

\( \Large \displaystyle [L]_{10} \equiv log_{10} [L] = log_{10} \frac{P_B \cdot K}{1 - P_B } \)

\( \Large \displaystyle \frac{P_B \cdot K}{1 - P_B } = 10^{[L]_{10}} \)

\( \Large \displaystyle P_B \cdot K = 10^{ [L]_{10}} - 10^{ [L]_{10}} \cdot P_B \)

\( \Large \displaystyle P_B \left( K + 10^{ [L]_{10}} \right) = 10^{ [L]_{10}}\)

\( \Large \displaystyle P_B = \frac{10^{ [L]_{10}}}{ K + 10^{ [L]_{10}} } = \frac{1}{ 1 + 10^{ -[L]_{10}} \cdot K } \)

となります．

ここで，常用対数と自然対数の関係から，

\( \Large \displaystyle 10^{-x} = e^y \rightarrow y = ln 10^{-x} = -x \ ln 10 \)

\( \Large \displaystyle 10^{-x} = e^y =e^{ -x \ ln 10} = e^{-2.3x} \)

となるので，

\( \Large \displaystyle P_B = \frac{1}{ 1 + e^{ -2.3 [L]_{10}} \cdot K } \)

ここで，分母のKも指数表示したいので，

\( \Large \displaystyle K = e^z\)

\( \Large \displaystyle ln K = z\)

\( \Large \displaystyle K = e^{ln K} \)

\( \Large \displaystyle log K = log e^z = z \ log e = 0.43 z \)

\( \Large \displaystyle z = \frac{1}{0.43} log K = 2.3 \ log K \)

\( \Large \displaystyle K = e^{2.3 \ log K} \)

として，

\( \Large \displaystyle P_B = \frac{1}{ 1 + e^{2.3 \ log K} e^{ -2.3 [L]_{10}} }= \frac{1}{ 1 + e^{ -2.3( [L]_{10} - log \ K)}} \)

となり， これはシグモイド型関数となります．

シグモイド曲線とは，

\( \Large \displaystyle y= \frac{1}{ 1 + e^{ - a( x - x_0)}} \)

であり，

x= -∞，においては，y = 0

x= ∞，においては，y = 1

x= x₀，においては，y=1/2

となります．

次に，常用対数表示の詳細について検討します．