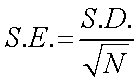
さて,一般によく使われるのが,標準偏差(S.D.),ですが,
標準誤差(S.E.)
というものもあります,その関係は,
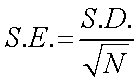
です.Nは試行回数,です.
ではいったい何が違うのでしょう?
・標準偏差
これは,
得られたデータがどのくらい散らばっているか
と言うもので,散らばりぐらいの程度を示します.
この散らばりは,データ数,試行回数,に依存しません.
たとえば,
インクを水の中に垂らし,一定時間後のインクの分布
を考えると,垂らしたインクの量に依存しないことが直感的にわかりますね.
・標準誤差
それに対して,標準誤差は,
繰り返し試行(実験)した際,その平均値がどの程度の確度を持っているか
というものです.
誤差を含む実験の場合,得られたデータにばらつきを生じます.
目的とする推定値は平均,として見積もるのですが,
少ない試行回数より多い試行回数の方が確実性を増す
というのも直感的に理解できると思います.
それが,分母のルートN,に効いてくるわけです.
つまり,
100回試行すれば,その信頼性は10倍に
10,000回試行すれば,その信頼性は100倍に
上がるわけです.
では,なぜ?ルートNなのでしょうか?
この概念は思ったより簡単で,誤差伝搬法則,より求めることができます.
試行回数N回行い,その平均値は,
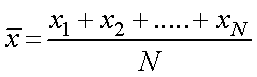
となります.
どの結果,xi,も同じ実験ですので,真の値Xは同じで,その分布σ,も同じです.
つまり,
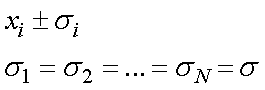
ですので,誤差伝搬法則の加算,を使って,
![]()
これを拡張すれば,誤差は,
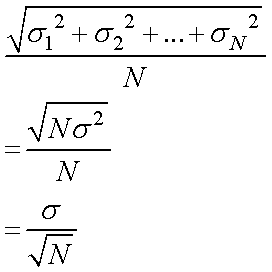
となるわけです.
この議論は,
誤差解析入門(東京化学同人)
を参考にさせていただきました.