偏光顕微鏡のなぞ-05

どの程度光が透過するか？

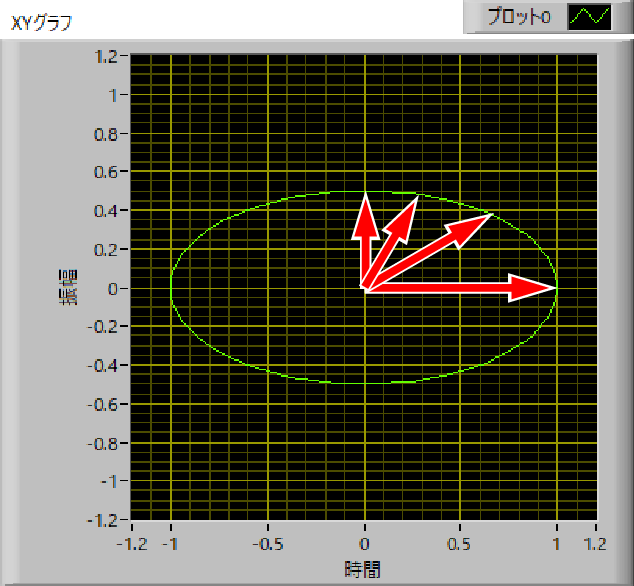
斜めの楕円では計算が面倒なので，水平な楕円を考えていきましょう．

この第一象限のX,Yのベクトルの大きさを比較すればいいのです．

しかし，円運動と違って角速度が角度によって変化してしまいますので，単純に積分することはできません．

X,Y，それぞれの波形は，

\(\Large x = E_{0x} \ cos (kz - \omega t + \delta_x) \)

\(\Large y = E_{0y} \ cos (kz - \omega t + \delta_y) \)

ここで，簡単に，z=0, E_0x=x₀, E_0y=y₀，δ_x=0，δ_y=π/2，とすれば，

\(\Large x = x_0 \ cos ( - \omega t) \)

\(\Large y = y_0 sin ( - \omega t ) \)

となります．

ここで，各時刻での偏光面の傾きを

\(\Large \alpha = \frac{y}{x} \)

とすれば，

\(\Large \alpha = \frac{y_0}{x_0} \ tan \omega t \)

となります．従ってそのときの角度，θ(t)は，

\(\Large \theta (t) = tan^{-1}\alpha = tan^{-1} \left[ \frac{y_0}{x_0} \ tan \omega t \right] \)

となります．また，

\(\Large x(t) = r(t) \ cos ( \theta) \)

\(\Large y(t) = r(t) \ sin ( \theta ) \)

で表すことができます．

この計算は解析的に解くことが（私には．．．）できませんので，Δｔを細かく刻んで，ｘ，ｙの総和を求めてその比を求めてみると，

\(\Large \frac{Sum \ of \ y}{Sum \ of \ x} = \frac{y_0}{x_0} \)

となることがわかりました．つまり，

つまり．．．．

　楕円の扁平率がクロスニコル状態での振幅の割合

　楕円の扁平率の二乗がクロスニコル状態での強度の割合

と考えて良さそうです．

楕円の扁平率と，xy平面上における位相差，との関係は．．．．．考えます．．．

ここ，を参考にすれば良さそうです．どうも答えは，

\(\Large sin \left( 2 \frac{y_0}{x_0} \right) = sin \left( \delta_y- \delta_x \right) \)

となるようです．