二次曲線のパラメータの推定
a1,をシフト
\(\Large \displaystyle y_i = a_0 + a_1 x_i + a_2 x_i^2 \)
| a0 | 6.1757 | 5.3774 | 4.5791 | 3.7808 | 2.9825 | |||
| a1 | -0.5851 | -0.0851 | 0.4149 | 0.9149 | 1.4149 | |||
| δ | -1 | -0.5 | 0 | 0.5 | 1 | |||
| a2 | 1.2602 | 1.2108 | 1.1614 | 1.1120 | 1.0627 | |||
| i | x | y | \( \hat{y} \) | |||||
| 1 | 0 | 5 | 6.175686 | 5.377409 | 4.579131 | 3.780811 | 2.982503 | |
| 2 | 2 | 10 | 10.04624 | 10.05043 | 10.0546 | 10.05875 | 10.0629 | |
| 3 | 3 | 15 | 15.76211 | 16.01937 | 16.27661 | 16.53384 | 16.79108 | |
| 4 | 4 | 25 | 23.99836 | 24.40993 | 24.82147 | 25.23302 | 25.64456 | |
| 5 | 6 | 50 | 48.03203 | 48.45592 | 48.87973 | 49.30361 | 49.72747 | |
| 6 | 9 | 102 | 102.9855 | 102.6871 | 102.3885 | 102.0901 | 101.7917 | |
| S (\(y_i - \hat{y} \)の平方和) | 7.812514 | 4.388513 | 3.2476 |
4.389923 | 7.815335 | |||
| dS (Seとの差分) | 4.564865 | 1.140864 | 0 | 1.142274 | 4.567686 | |||
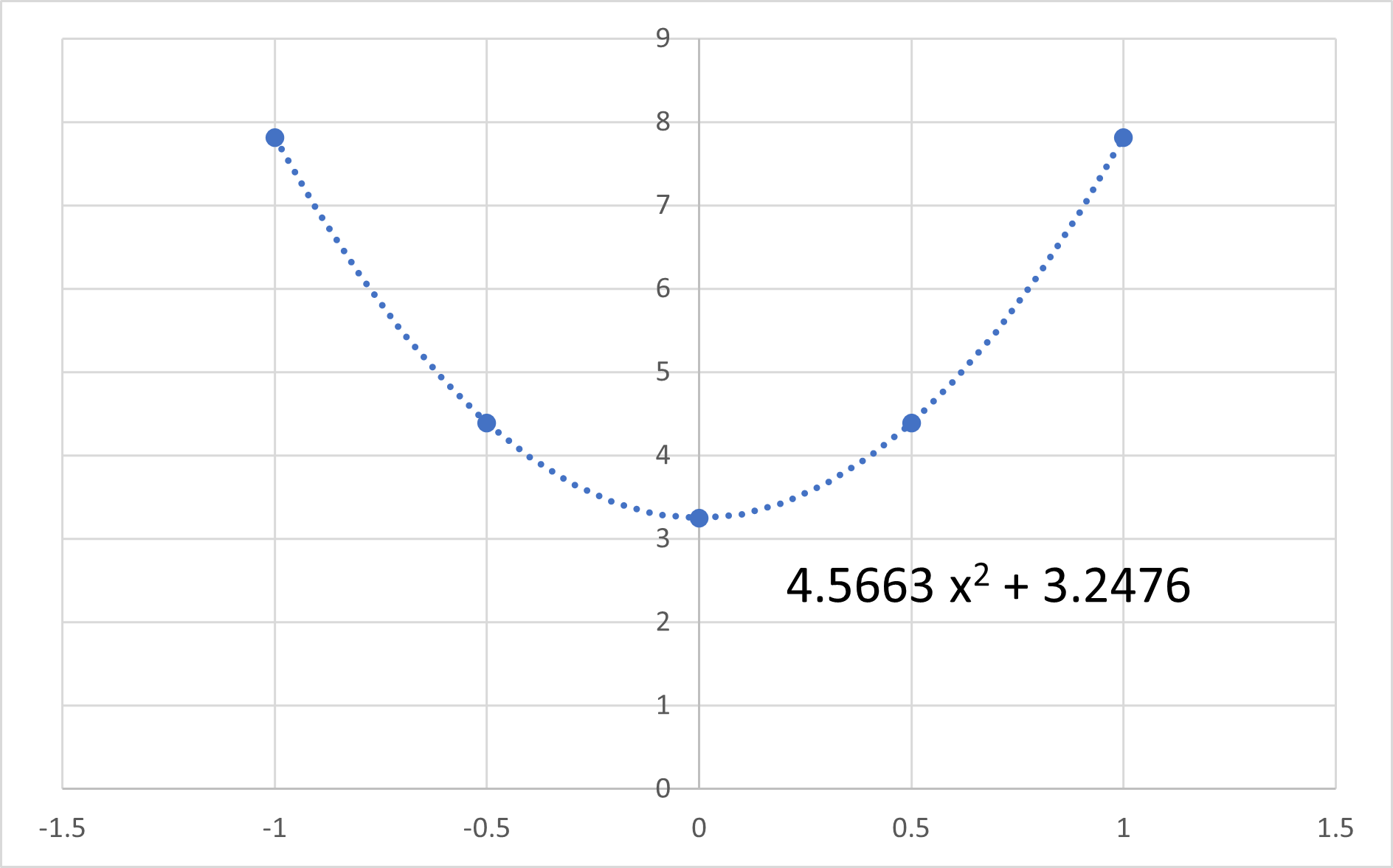
切片を変えて傾きを近似すると,このようなグラフを得ることができます.
ここで,S,Se,は,
・残差平方和
推定値からの残差
\(\Large \displaystyle Se = \sum_{i=1}^{n} \left( y_i -\hat{a_0} - \hat{a_1} x_i - \hat{a_2} x_i^2 \right)^2 \)
a0をシフトさせたときの,推定値からの残差
\(\Large \displaystyle S = \sum_{i=1}^{n} \left( y_i -\hat{a_0} - a_1 x_i - \hat{a_2} x_i^2 \right)^2 \)
であり,傾きの値a1を,δ,だけシフトさせて,固定し,その際のa0, a2の推定値をソルバーで推定しました.
dS,を見ていただけるとわかるように,推定値,Seが一番小さく,ほぼ左右対称に増加していることがわかります.
グラフ化すると,

のように,二乗+定数できれいに近似できます(xの項があるのはエクセルでべき乗で近似したため...)
二次曲線の近似においてもきれいに近似でき,
\(\Large \displaystyle y = 3.2476 + 4.5662 \ \delta^2 \)
ここで,分散値は,
・分散
\(\Large \displaystyle Ve = \frac{1}{n-3} \sum_{i=1}^{n} \left(y_i -\hat{a_0} - \hat{a_1} x_i \right)^2 = \frac{Se}{n-2} = \frac{3.2476}{6-3} = 1.0826 \)
であり(a0,a1,の二つのパラメータが2つあるので,自由度は,n-3),
\(\Large \displaystyle 4.5662 \ \delta^2 = 1.0826 \)
となるδがSEとなるので,
\(\Large \displaystyle \delta^2 = \frac{1.0826}{4.5662} = 0.2371 \)
\(\Large \displaystyle SE_{a_0} = \sqrt{\delta^2} = 0.4869 \)
と推定できます.
・Rによる推定
Rでの近似を行ってみると,
プログラムは,
xx <- c(0,2,3,4,6,9)
yy <- c(5,10,15,25,50,102)
plot(xx,yy)
fm<-nls(yy~a0+a1*xx+a2*xx^2,start=c(a0=5,a1=1,a2=1),trace=TRUE)
summary(fm)
で,結果は,
| Parameters: | |||||
| Estimate | Std. Error | t value | Pr(>|t|) | ||
| a0 | 4.57931 | 0.96042 | 4.768 | 0.01752 | * |
| a1 | 0.41473 | 0.4869 | 0.852 | 0.45693 | |
| a2 | 1.16144 | 0.05045 | 23.022 | 0.00018 | *** |
とドンピシャ一致することがわかります.
Kyplotにおいても,
| 推定値 | 標準誤差(SE) | |
| A1 | 4.57931 | 0.96042 |
| A2 | 0.414734 | 0.486903 |
| A3 | 1.161442 | 0.05045 |
と同じ結果となります(ということはこの二つのソフトは同じアルゴリズムで標準誤差を計算?)
次は,a2,をシフトしてみましょう.