ガウス積分
ガウス積分,を解いていきましょう.
\(\Large \displaystyle \int_{- \infty}^{\infty} e^{-k x^2} dx = \sqrt { \frac{ \pi}{k}} \)
同じものの積を取ると,
\(\Large I = \displaystyle \int_{- \infty}^{\infty} e^{-k x^2} dx \)
\(\Large \begin{eqnarray} I^2
&=& \displaystyle \int_{- \infty}^{\infty} e^{-k x^2} dx \ \displaystyle \int_{- \infty}^{\infty} e^{-k y^2} dy \\
&=& \displaystyle \int_{- \infty}^{\infty} \displaystyle \int_{- \infty}^{\infty} e^{-k (x^2 + y^2)} dx dy \\
\end{eqnarray} \)
ここで,円柱座標表示を考えます.

\(\Large x = r \ \cos \theta \ y = r \ \sin \theta \)
微小領域,ds,を考えると,
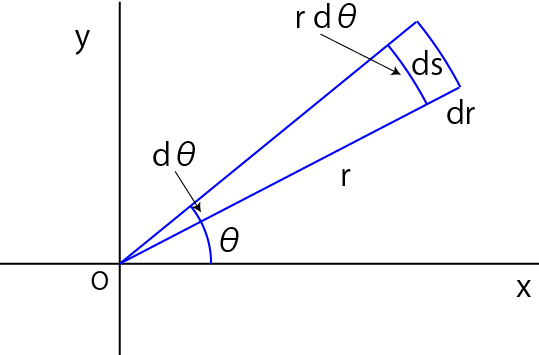
\(\Large \begin{eqnarray} ds
&=& \pi (r + dr)^2 \times \frac{ d \theta }{2 \pi} - \pi r^2 \times \frac{ d \theta }{2 \pi} \\
&=& \left[
(r + dr)^2 - r^2 \right] \times \frac{ d \theta }{2} \\
&=& \left[
2 r dr + (dr)^2 \right] \times \frac{ d \theta }{2} \\
&=& r dr d \theta + \frac{1}{2} (dr)^2 d \theta \\
\end{eqnarray} \)
第二項は無視して,
\(\Large ds = dx \ dy = r \ dr \ d \theta \)
となります.積分範囲は,
\(\Large- \infty \hspace{ 4pt } \rightarrow \hspace{ 6pt } x \rightarrow \infty \\
\Large \hspace{ 16pt } 0 \hspace{ 8pt } \rightarrow \hspace{ 4pt } \theta \hspace{ 5pt }\rightarrow 2 \pi \\
\Large \hspace{ 16pt } 0 \hspace{ 8pt } \rightarrow \hspace{ 4pt } r \hspace{ 5pt }\rightarrow \infty \)
となります.
座標変換して,
\(\Large \begin{eqnarray} I^2
&=& \displaystyle \int_{- \infty}^{\infty} \displaystyle \int_{- \infty}^{\infty} e^{-k (x^2 + y^2)} dy \\
&=& \displaystyle \int_{0}^{\infty} \displaystyle \int_{0}^{ 2 \pi} e^{-k r^2} \ dr \ d \ \theta \\
&=& 2 \pi \displaystyle \int_{0}^{\infty} e^{-k r^2} r \ dr \\
\end{eqnarray} \)
ここで,
\(\Large Y \equiv e^{-k r^2} \)
\(\Large dY = -2 \ k \ r \ e^{-k r^2} \ dr \)
となります.積分範囲は,
\(\Large 0 \hspace{ 8pt } \rightarrow \hspace{ 4pt } r \hspace{ 5pt }\rightarrow \infty \\
\Large \hspace{ 0pt } 1 \hspace{ 8pt } \rightarrow \hspace{ 4pt } Y \hspace{ 5pt }\rightarrow 0 \)
となりますので,
\(\Large \begin{eqnarray} I^2
&=& 2 \pi \displaystyle \int_{0}^{\infty} e^{-k r^2} r \ dr \\
&=& 2 \pi \displaystyle \int_{1}^{0} - \frac{1}{2 k} \ dY \\
&=& 2 \pi [ Y ]_1^0 \left(- \frac{1}{2 k} \right) \\
&=& \frac{ \pi}{k} \\
\end{eqnarray} \)
従って,
\(\Large I = \sqrt{\frac{ \pi}{k} } \)
\(\Large \displaystyle \int_{- \infty}^{\infty} e^{-k x^2} dx = \sqrt { \frac{ \pi}{k}} \)
となります.