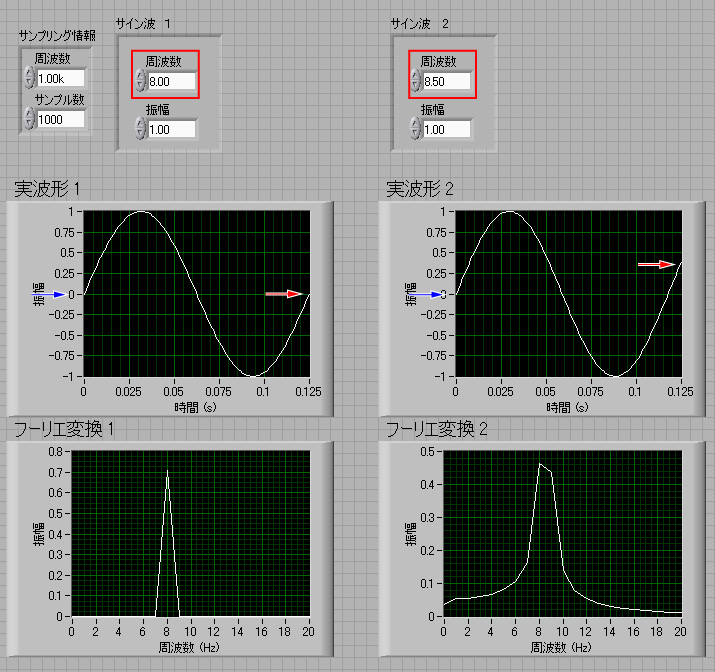
さて,下のフーリエ変換の図をご覧ください.

下のフーリエ変換のグラフを見ると,明らかに,左の方がシャープですね.
何が違うのでしょう?
それは,赤枠で囲んだ,
サイン波の周波数
が違うのです.
それ以外の,サンプリング周波数,サンプル数,振幅,は全く一緒です.
この二つ,なんで周波数だけの違いで,これほど差があるのでしょう?
それは,青矢印と赤矢印を注意してください.
もし,この実波形を2枚横に並べてみると,
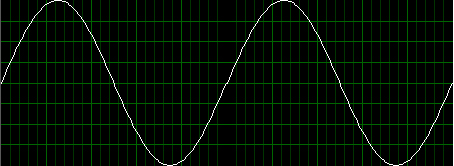
左の図では,青矢印と赤矢印が連続してつながる
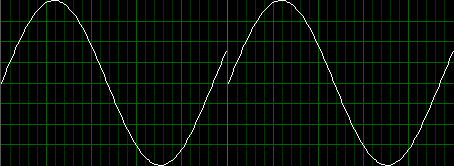
右の図では,青矢印と赤矢印は連続してつながらない
となります.
この不連続さが,データをゆがめてしまっているのです.
元々,フーリエ変換はある波形を与えたとしても,その左右に同じものが連続し存在する,として計算しています.
ですので,この不連続さがあると,不連続さも信号として計算してしまうのです.
そうそう,得られた波形にぴったり来る周波数を見ることは実験状マレです.
では,どうすればよいのでしょう?
そこで登場するのが,
窓関数
です.
窓関数とは,波形を無理矢理つなげるようなものです.
両端を,0,にしてしまえばいいのです.
それを示したのが,下の図です.
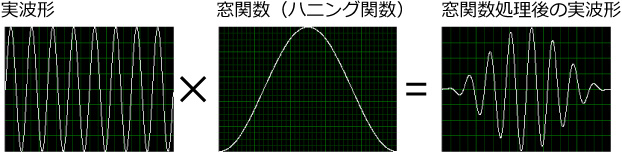
こうすれば,どんな関数でも,両端は値が0,傾きも0なので,並べても連続的につながります.
ちなみに,窓関数はいろいろありますが,代表的な窓関数,ハニング関数,を示しました.
このカーブはコサイン関数で,
![]()
となります.
その効果を実際の波形で見てみましょう.
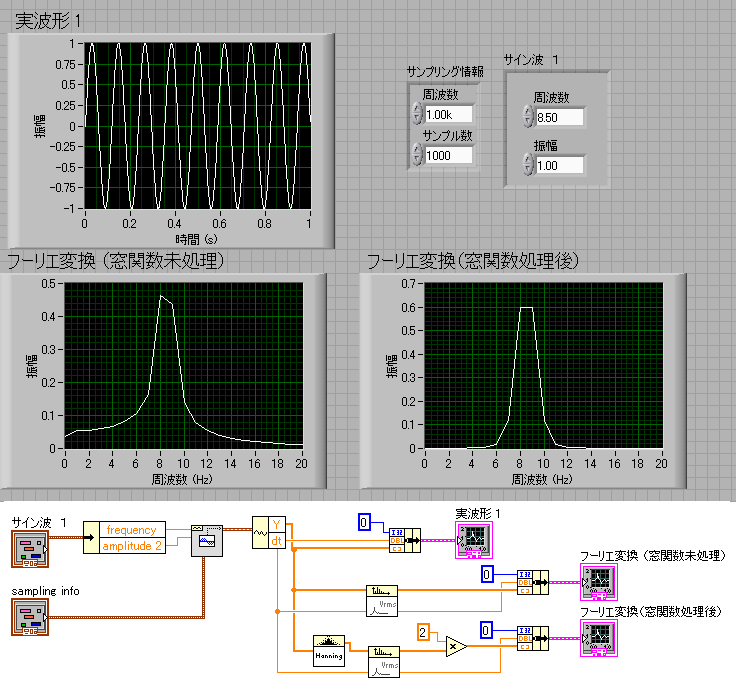
左が窓関数未処理,右が窓関数処理後,です.
ピークの鋭さはあまりよくありませんが,すそ野の切れがいいことがわかりますね.
ちなみに,プログラムを見ると,窓関数処理後のスペクトル波形に2倍しているのが見えますね.
これは,窓関数で処理したため,実際の振幅が小さくなってしまった影響を回復させるためです.
ハニング関数を見ればわかるように,ちょうど1/2の面積になっていることがわかりますね.
この値は窓関数によって変わります.
では,パワースペクトルの場合の補正を考えましょう.