エバネッセント光の減衰
授業なので,エバネッセント光の減衰は指数関数的になる,数十~百ナノメートル程度である,と説明していますが,ちゃんと計算したことがなかったのでトライしてみました.
本来は電磁気学で解く問題かもしれませんが....できれば波動光学で解きたい....
一分子生物学(化学同人),の第14章に波動光学で解けるとあったのですが,残念ながら私には解けませんでした.
そこで,顕微分光法 第10巻(講談社),を参考に計算してみました(一部座標軸の表示,屈折率など変更しています)

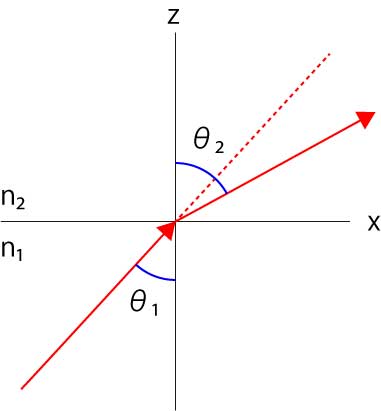
まず,X軸を境に異なる屈折率を横切る光線を考えます.
スネルの法則から,
\(\Large n_1 \ sin \theta_1 = n_2 \ sin \theta_2 \)
となります.また,n1>n2,とします.
それぞれの空間で伝搬する平面波の振動は,
入射光:\(\Large u_1 \ (x,z,t) = A_0 \ exp \left[ i \left( n_1 k_0 cos \theta_1 \cdot z+n_1 k_0 sin \theta_1 \cdot x- \omega t \right) \right] \)
透過光:\(\Large u_2 \ (x,z,t) = B_0 \ exp \left[ i \left( n_2 k_0 cos \theta_2 \cdot z+n_2 k_0 sin \theta_2 \cdot x- \omega t \right) \right] \)
となります,ここでk0は光の波数で,2π/λ0です,それぞれの媒質の屈折率によって変化していることがわかります.
・全反射
入射角を大きくしていくと,
\(\Large sin \theta_2 = 1 \)
となり,屈折した光は界面の境界上を平衡に伝搬するようになります. このときの入射角を臨界角と呼び,
\(\Large sin \theta_c = \frac{n_2}{n_1} \)
となります.
\(\Large sin^2 \theta_2 + cos^2 \theta_2= 1 \)
の関係から,
\(\Large cos^2 \theta_2= 1 - sin^2 \theta_2 = 1- \left( \frac{n_1}{n_2} sin \theta_1 \right)^2 \)
\(\Large cos \theta_2=\sqrt{ 1- \frac{n_1^2}{n_2^2} sin^2 \theta_1 } = i \sqrt{ \frac{n_1^2}{n_2^2} sin^2 \theta_1 -1} = i \frac{n_1}{n_2} \sqrt{ sin^2 \theta_1 -\frac{n_2^2}{n_1^2}}\)
となります.
・透過光
透過光:\(\Large u_2 \ (x,z,t) = B_0 \ exp \left[ i \left( n_2 k_0 cos \theta_2 \cdot z+n_2 k_0 sin \theta_2 \cdot x- \omega t \right) \right] \) は,
\(\Large u_2 \ (x,z,t) = B_0 \ exp \left[ i \left( n_2 k_0 \left\{i \frac{n_1}{n_2} \sqrt{ sin^2 \theta_1 -\frac{n_2^2}{n_1^2}} \right\} \cdot z+n_2 k_0 sin \theta_2 \cdot x- \omega t \right) \right] \)
\(\Large =
B_0 \ exp \left[ - n_1 k_0 \sqrt{ sin^2 \theta_1 -\frac{n_2^2}{n_1^2}} \cdot z \right] exp \left[ i \left( n_2 k_0 sin \theta_2 \cdot x- \omega t \right) \right] \)
と振幅と振動に分けることができます. 光強度は振幅の二乗となるので, 強度は,
\(\Large I = \left\{ B_0 \ exp \left[ - n_1 k_0 \sqrt{ sin^2 \theta_1 -\frac{n_2^2}{n_1^2}} \cdot z \right] \right\}^2 \)
\(\Large = B_0^2 \ exp \left[ - 2 n_1 k_0 \sqrt{ sin^2 \theta_1 -\frac{n_2^2}{n_1^2}} \cdot z \right] \)
となります.減衰率(e-1となる距離)は,
\(\Large \tau = \frac{1}{ 2 n_1 k_0 \sqrt{ sin^2 \theta_1 -\frac{n_2^2}{n_1^2}} } \)
となります.波数,\(\Large k_0 = \frac{2 \pi}{\lambda_0}\),から,
\(\Large \tau =
\frac{\lambda_0}{4 \pi n_1} \frac{1}{ \sqrt{ sin^2 \theta_1 -\frac{n_2^2}{n_1^2}} } \)
\(\Large =
\frac{\lambda_0}{4 \pi n_1} \frac{1}{ \sqrt{ sin^2 \theta_1 -sin^2 \theta_c} } \)
もしくは,
\(\Large = \frac{\lambda_0}{4 \pi } \frac{1}{ \sqrt{ n_1^2 sin^2 \theta_1 -n_2^2 } } \)
となり,ここなど,に示されている式となります.
・実際の侵入長
n1=1.515(ガラス),n2=1.33(水)を入れると,
\(\Large sin \theta_c = 61.39 \)度
波長を532nm,とすると最小の侵入長は,θcが1となる角度であるので,58.35nm,となります.
ちなみに,入射角を70度とすると,83.37nm,となります.
全反射ギリギリ,入射角を62度とすると,296nm,となります.