まずは回転から.
\(\Large \gamma_{rot} = \frac{ \frac{1}{3} \pi \eta L^3}{ln(L/(2r))-0.66} \)
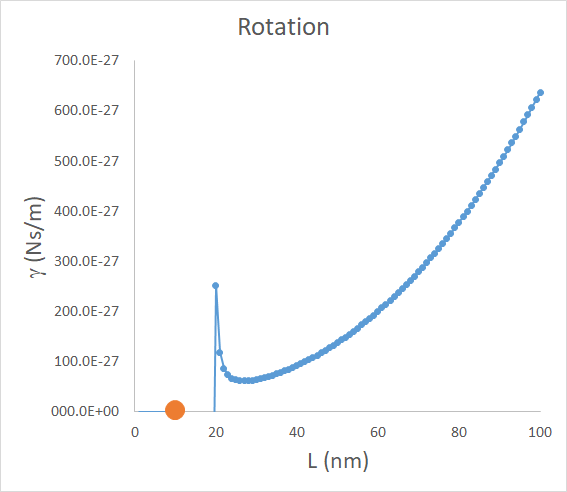
において,r = 5 nm, L = 0 - 100 nm,の領域で計算してみると,

となり,Lがどんどん小さくなると急激に値が変化します.これは,分母のlnの部分の影響です.
オレンジの丸は,
 と
と それぞれの粘性抵抗係数が,が2r=Lにおいて等しいと仮定した場合の点です.
それぞれの粘性抵抗係数が,が2r=Lにおいて等しいと仮定した場合の点です.
ですので,L≒rの場合にはこの式は適用できないことになります.どうしたらよいでしょう?
そういうときには原点に戻れ,ということで元論文をもう一度見て
Rotational dynamics of rigid, symmetric top macromolecules. Application to circular cylinders
Mana M. Tirado and Jose Garcia de la Torre, J. Chem. Phys. 73(4), 15 Aug. 1980
を見てみると,Table II.,に,
| p-1 | δ⊥ |
0.50 |
-0.216 |
0.45 |
-0.260 |
0.40 |
-0.303 |
0.35 |
-0.348 |
0.30 |
-0.392 |
0.25 |
-0.436 |
0.20 |
-0.481 |
0.15 |
-0.526 |
0.10 |
-0.571 |
0.05 |
-0.616 |
0 |
-0.662 |
なる表があります.
\(\Large p = L/(2r) \)
と定義されていますので,Lが十分長い場合(p-1=0)には上記式の分母の係数,-0.66,と一致します.
このテーブルの関係は,
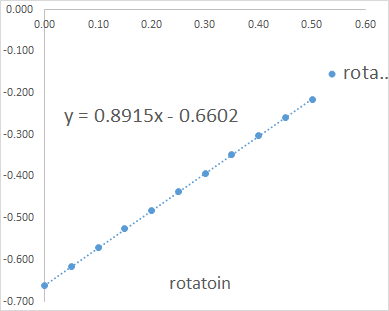
と直線関係になるので,上記の式を変形してみましょう.すると,
\(\Large \gamma_{rot} = \frac{ \frac{1}{3} \pi \eta L^3}{ln(L/(2r)) + 0.8915 \frac{2r}{L} - 0.66} \)
となります.この式を描いてみると,
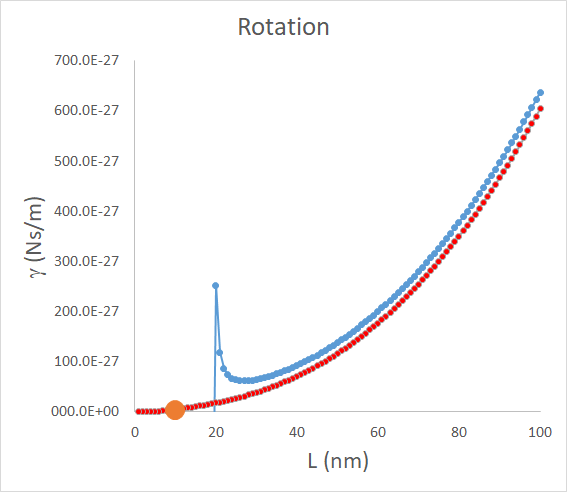
となり,かなりいい感じとなります.
しかし,たぶんこの論文に描かれているこの表は理論的・実験的な根拠があるわけではなく,多項式近似式を当てはめただけと思いますので,便宜上と思われます.
では,並進の場合を考えていきましょう.