直方体,立方体,底面が平行四辺形,ひし形の際に成り立つ公式の導出を行いました.
ポイントは,
底面積を三角形で分割,さらには分割した三角形の面積が等しい
場合に,成り立つ公式でした.
さらには,正多面体を底面積に持つ立体も適用できそうです.
なので,台形,を底面に持つ立体は適用できない,ことになります.
しかし,全くお手上げなのでしょうか?
・台形
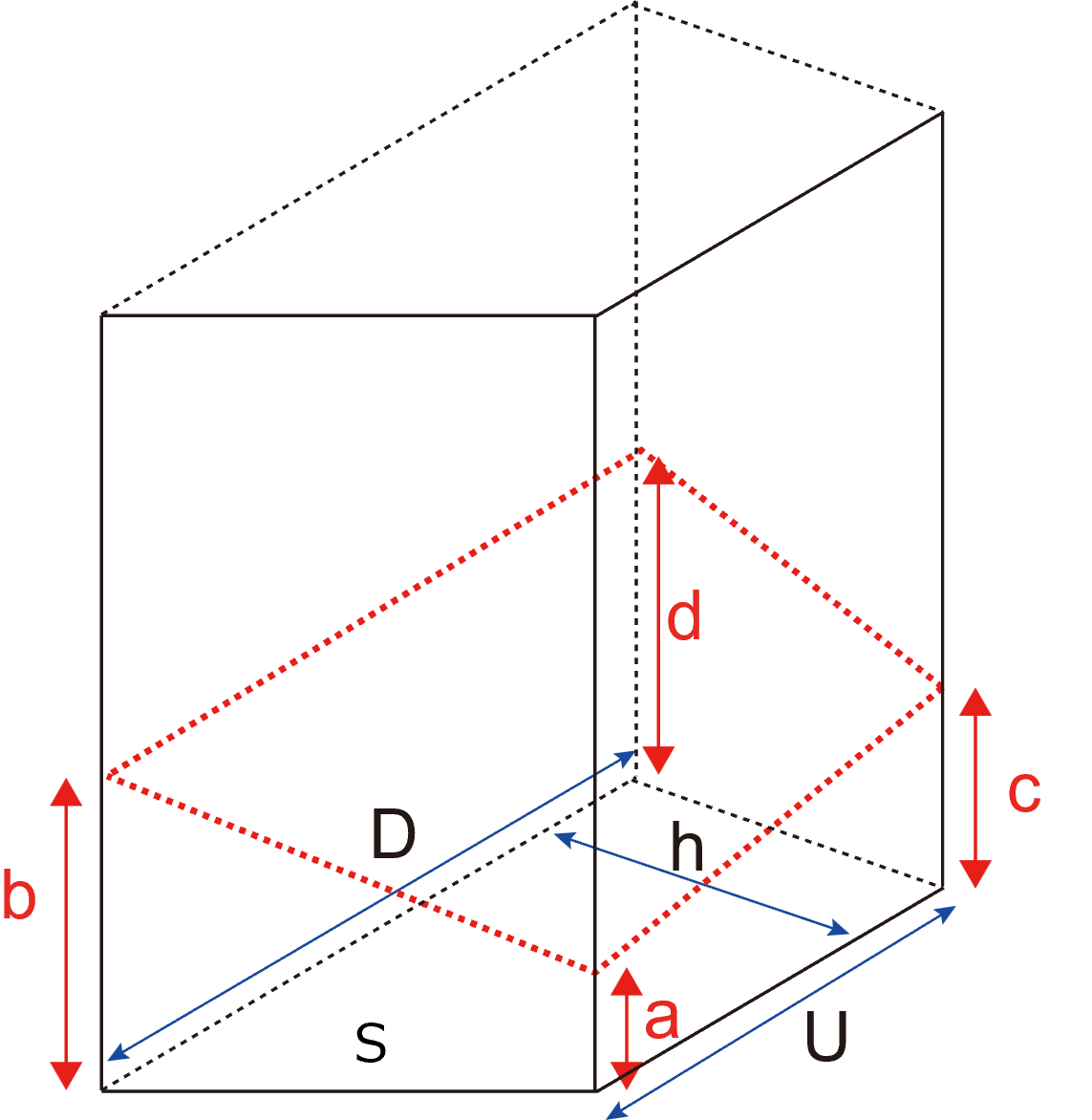
台形を底面に持つ立体(とりあえず,90度でそびえたつ)を斜めに切断した場合の体積です.

底面の台形は,
面積 : S
上辺 : U
底辺 : D
高さ : h
上辺と底辺は平行
とし,a, b, c, d, が断面となります.
この4点も独立ではなく,3点決まると残りの1点が決まります.補助線を加えると,
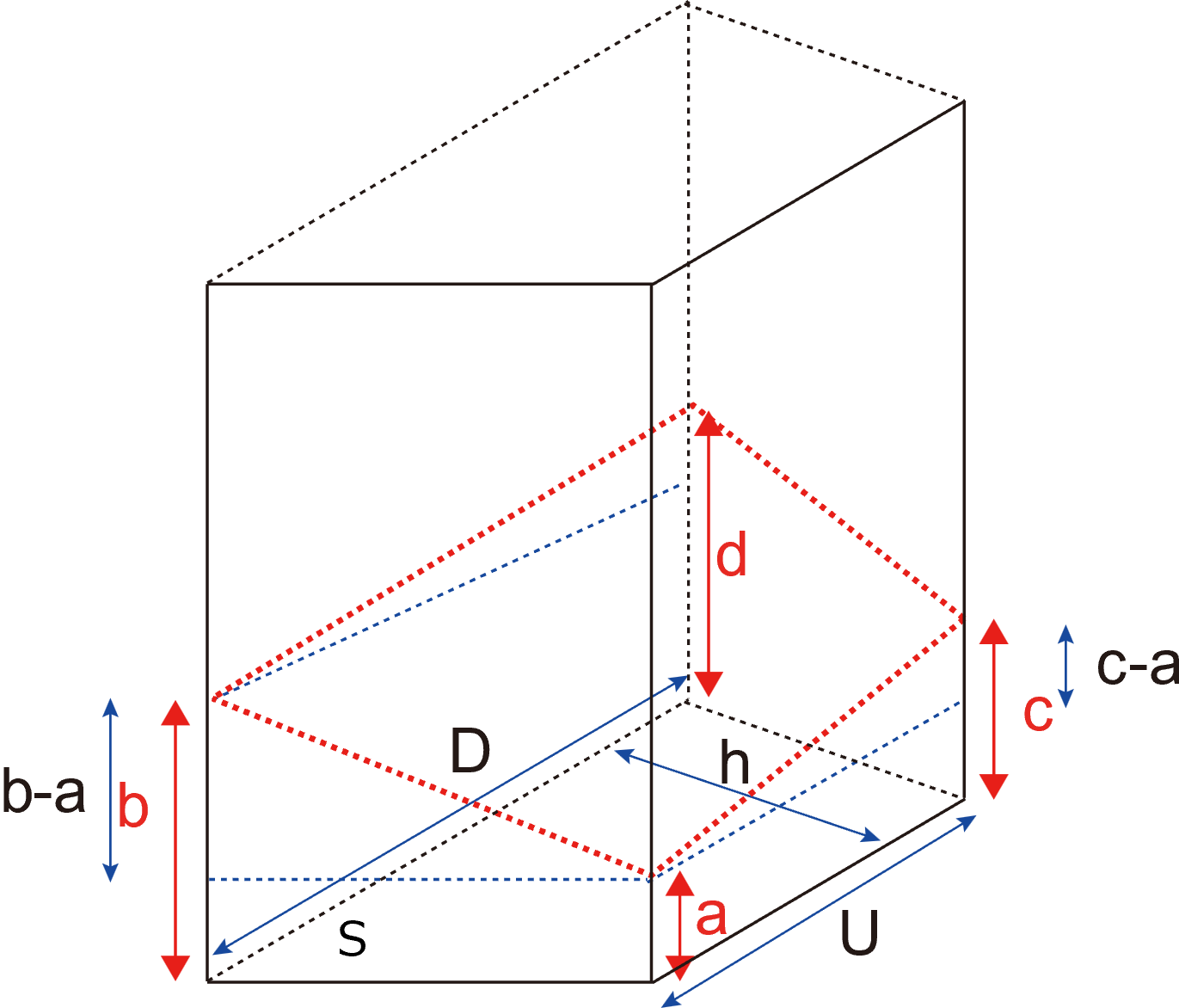
となります.上辺と底辺の断面線は平行となりますが,そこからできる三角形は相似でありますが,合同ではありません
そこで,dとbの差分を考えると,
\( \Large \displaystyle d - b= \frac{c-a}{U} \cdot D \)
となります.
直方体と同様に,三角柱に切り分けていきます.
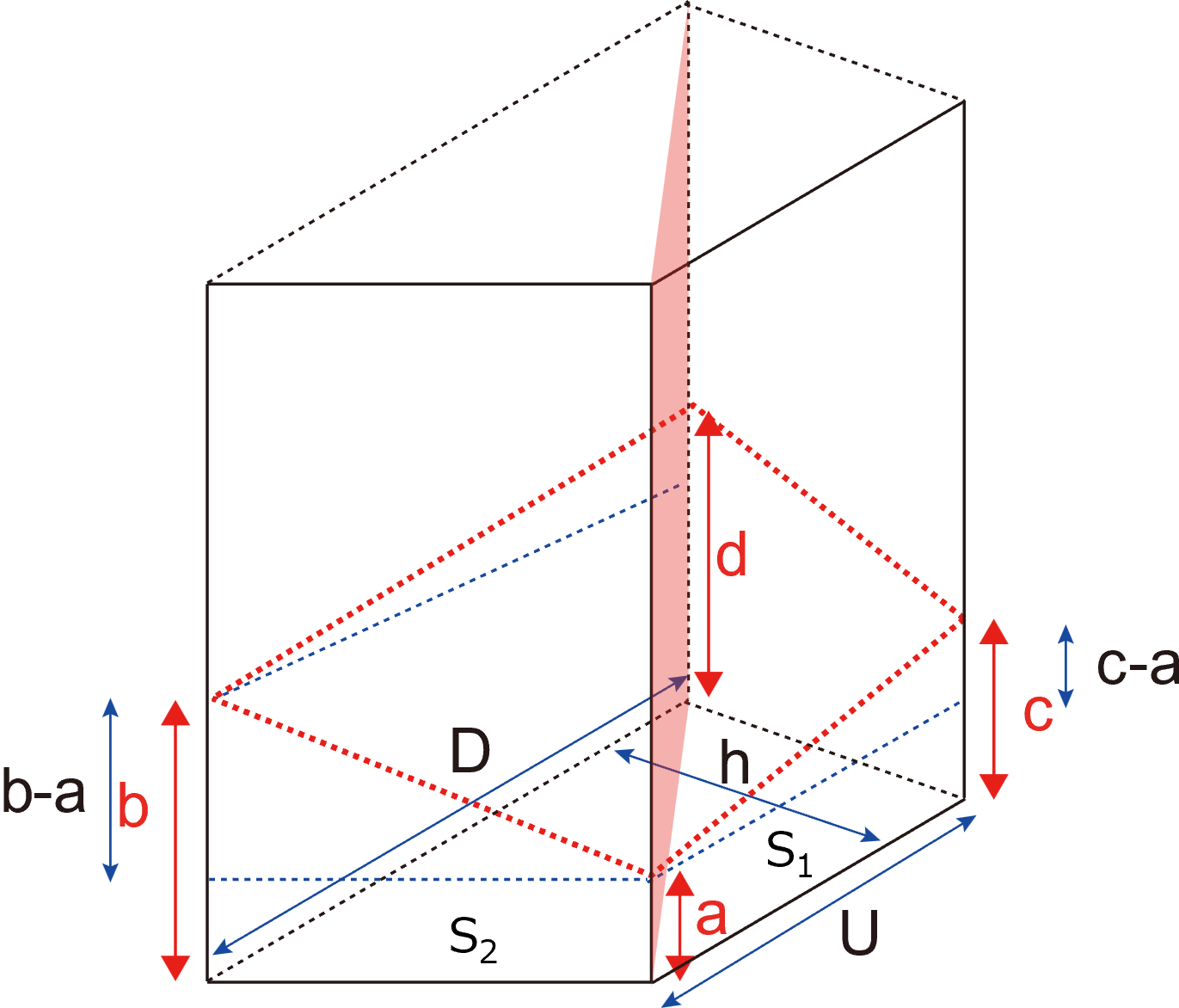
各底面積を,S1, S2, とすると,
\( \Large \displaystyle S = S_1 + S_2 = \frac{U + D}{2} h\)
\( \Large \displaystyle S_1 = \frac{U }{2} h\)
\( \Large \displaystyle S_2 = \frac{D }{2} h\)
となりますので,
\( \Large \displaystyle V_1 = S_1 \frac{a+c+d}{3} \)
\( \Large \displaystyle V_2 = S_2 \frac{a+b+d}{3} \)
\( \Large \displaystyle V = V_1 + V_2 = S_1 \frac{a+c+d}{3} +S_2 \frac{a+b+d}{3}\)
\( \Large \displaystyle= \frac{U }{2} h \frac{a+c+d}{3} +\frac{D }{2} h \frac{a+b+d}{3}\)
\( \Large \displaystyle= \frac{h }{6} [ U(a+c+d) + D (a+b+d)] \)
とあまりきれいな形とは言えませんが,計算式を導出することができました.