
・直方体
次は直方体を斜めに切断した場合の体積です.
底面積をS,直方体なので,底面は長方形となり,それぞれの長さをw,d,とします.

直方体の縦4辺を横切る断面なので,a, b, c, dの4点が存在することになりますが,どんな点をとってもいいわけではなく,
平面にするためには3点を決めると残りの点の高さが決まります.
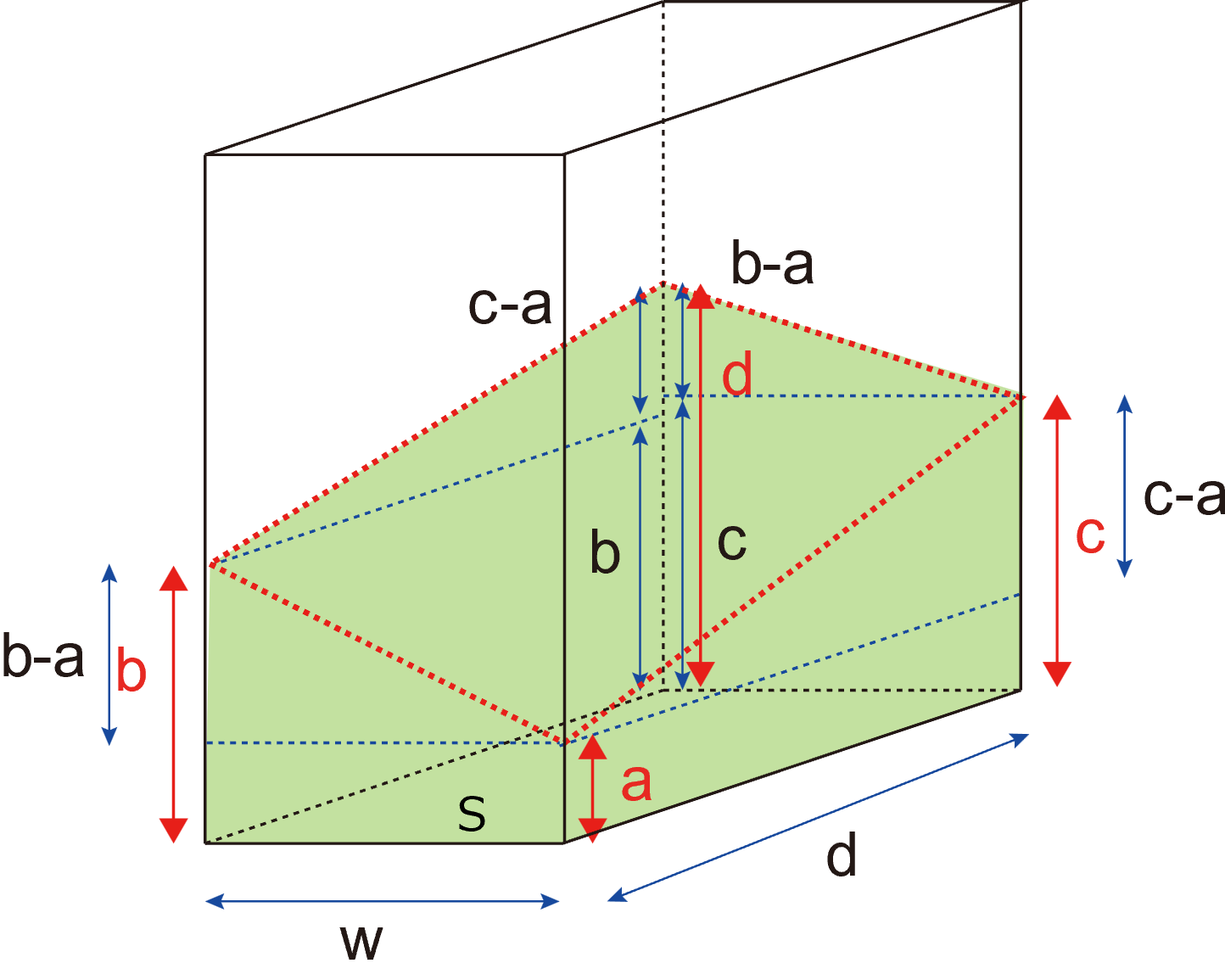
a, b, c,それぞれに底面と平行な補助線を引くと,それぞれの三角形の合同から,
\( \Large \displaystyle d = b-a+c = c-a+b \)
\( \Large \displaystyle a + d = b + c \)
が成り立つことがポイントとなります.
三角柱の場合のように,どのように分割して体積を求めようかな?と考えていたのですが,ふと..
直方体をに分割したら二つの三角柱になるのでは?
と気づきました.
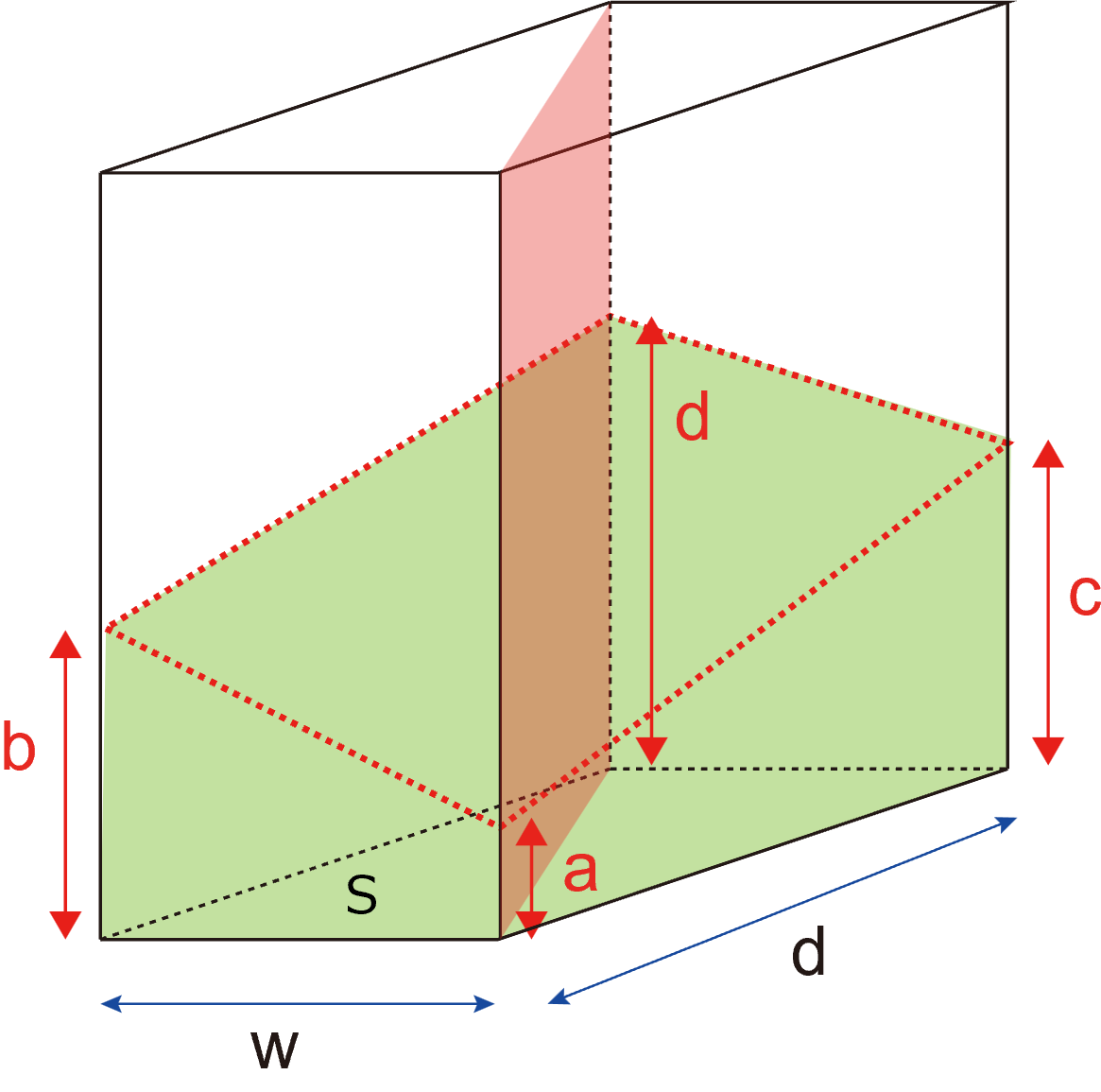
赤面が断面です.底面が長方形なので,それぞれの底面積は等しくなり,S/2,となります(これがポイント)
それぞれの三角柱の体積は,
\( \Large \displaystyle V = V_1 + V_2 = \frac{a+b+d}{3} \frac{S}{2} + \frac{a+c+d}{3} \frac{S}{2} \)
\( \Large \displaystyle = \frac{2a+b+c+2d}{6} S \)
\( \Large \displaystyle = \frac{3a+3d}{6} S \)
\( \Large \displaystyle = \frac{a+d}{2} S \)
\( \Large \displaystyle = \frac{(a+d)+(a+d)}{4} S \)
\( \Large \displaystyle = \frac{a+b+c+d}{4} S \)
この計算のポイントは,
分割した底面積が等しい
点にあります.つまり,
立方体,直方体,さらには,平行四辺形,ひし形,のみ成り立つ公式
と言えます.ちなみに,台形で同様の計算を試みたところ,結構複雑な計算式となってしまいました.
次は,正多角形を底面に持つ立体です.これは,自分自身の計算では成り立ちましたが,ネットを見てもそのような記述が見当たらず,本当に正しいかはちょっと不安です.