エクセルでの近似 - R二乗値の求め方 - 02

次には，

・基本の直線近似（切片なし）

\( \Large \displaystyle y=ax \)

で．
　a = 1
でランダム関数によりばらつきを与えています．

\( \Large \displaystyle R^2=\color{red}{0.9968} \)

相関係数は，

\( \Large Cov = \frac{\displaystyle \sum_{i=1}^n (x_i - \overline{x})(y_i - \overline{y}) }{\sqrt{\displaystyle \sum_{i=1}^n (x_i - \overline{x} )^2} \sqrt{\displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2} } = 0.9940\)

\( \Large Cov^2 = \color{blue}{ 0.9881} \)

となり，一致しません．

決定係数，R₁²，は，

\( \Large R_1^2 = 1 - \frac{\displaystyle \sum_{i=1}^n (y_i - \overline{y})^2 }{\displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2} = \color{blue}{0.9843} \)

となり，一致しません．

しかし，決定係数，R₇²，は，

\( \Large R_7^2 = 1 - \frac{\displaystyle \sum_{i=1}^n (y_i - \overline{y})^2 }{\displaystyle \sum_{i=1}^n y_i -^2} = \color{red}{0.9968} \)

となり，直線近似（切片あり)は，決定係数，R₇²，を示すものと思われます．

次に，

・基本の直線近似（切片固定）

場合はどうなるのでしょう？

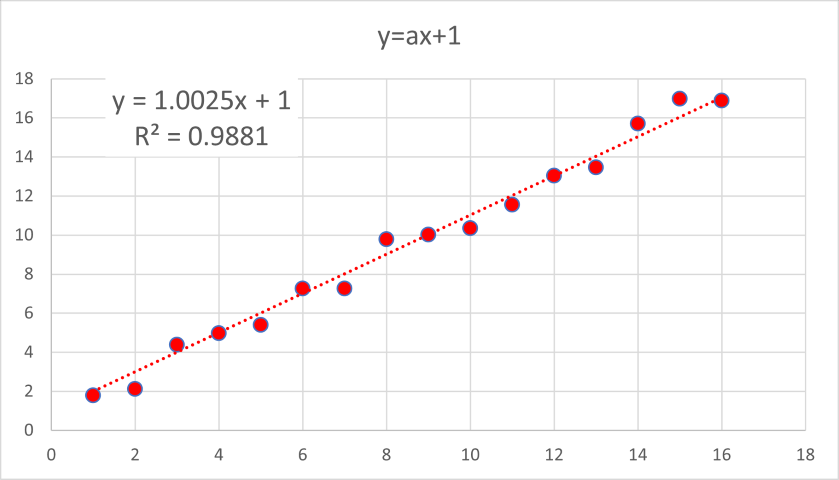
\( \Large \displaystyle R^2=0.9881 \)

相関係数は，

\( \Large Cov = \frac{\displaystyle \sum_{i=1}^n (x_i - \overline{x})(y_i - \overline{y}) }{\sqrt{\displaystyle \sum_{i=1}^n (x_i - \overline{x} )^2} \sqrt{\displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2} } = 0.9940\)

となり，

\( \Large Cov^2 = \color{red}{0.9881} \)

となり，一致します．

決定係数，R₁²，は，

\( \Large R_1^2 = 1 - \frac{\displaystyle \sum_{i=1}^n (y_i - \overline{y})^2 }{\displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2} = \color{red}{0.9881} \)

となり，直線近似（切片固定)は，決定係数，R₁²，を示すものと思われます．

・理由

なぜ，切片のあるなしで計算方法が違うのか，この違いについては，いろいろなサイトに載っていますが，

　マイクロソフト

自体にも記載があります，バージョンによって異なるようです（今回検証したのは365）．

どうも別のソフト（検証したのは，R）も同様の計算方法のようです．

なぜか，という点については，ここ，に説明がありましたが，私の読解力では読み解けませんでした（計算式に，二乗，が入っていないのはなぜだろう？）

こちらのサイト，にも記載がありましたが，なぜか，についての記載はないようです．

今のところ，私の理解力では，そういうものなのだ，というように理解していくしかなさそうです．